Центрированная оптическая система. Кардинальные элементы ЦОС: фокусы, фокальные плоскости, главные точки и главные плоскости, узловые точки.

Световым лучом считаем линию, по которой распространяется энергия световой волны. Совокупность лучей образуют световой пучок. Будем рассматривать гомоцентрические и параллельные пучки лучей.

Если световые лучи (или их продолжения) выходят из одной точки, то пучок гомоцентрический.

Оптическая система представляет собой совокупность оптических деталей, предназначенных для преобразования световых пучков путём преломления и отражения.

Если центры всех оптических поверхностей лежат на одной прямой, называемой оптической осью, то такая система называется центрированной оптической системой.

Любая оптическая система производит преобразование – предмет изображения.

Если каждой точкой предмета соответствует изображение тоже в виде точки и сохраняется геометрическое подобие, то такая система называется идеальной.

Чтобы подчеркнуть тот факт, что точка предмета изображается системой в виде точки, говорят, что это изображение стигматическое (точечное). Такая точка и её изображение называются сопряжёнными.

Пространство, где могут находиться точки предмета, называется пространством предмета.

Точки пространства, в которых может находиться точки изображения, называются пространством изображения.

Большинство реальных оптических систем можно считать идеальными только для параксиальных (приосевых) лучей, т.е. лучей, которые образуют малые углы с оптической осью и с перпендикулярами к оптическим поверхностям.

Параксиальными являются лучи, при которых выполняется sinα=tgα=α.

Свойства центрированных оптических систем можно полностью определить, если задать координальные моменты – передние и задние фокусы, главные и узловые точки, соответствующие плоскости.

Фокусы оптической системы и фокальные плоскости.

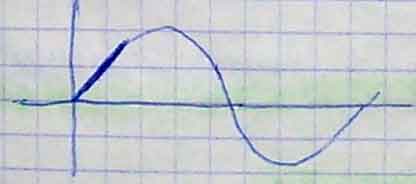
Если на оптическую систему пустить пучок параллельных лучей, причём параллельных главной оптической оси, то они сойдутся в точке, называемой задним фокусом оптической системы.

Задний фокус можно считать изображением сопряжённой бесконечной удалённой точки, находящейся на оптической оси. Отметим, что если фокус образован пересечением продолжений лучей, то задний фокус может находиться и перед системой.

Если параллельный пучок лучей направить со стороны изображения, то они сойдутся в точке – переедем фокусом оптической системы.

Передним фокусом можно считать и точку, сопряжённая в которой точка изображения находится на бесконечности ((на оптической оси). В плоскости, проведённая перпендикулярно оптической оси в заднем и передним фокусе, называется задней и передней фокальной плоскостью.

Под линейным увеличением Г понимают отношение размера изображения к размеру предмета.

Г=y'/y. Будем считать все отрезки или предметы, находящиеся выше оси положительными (+), а ниже – отрицательными (-). Существуют две сопряжённые плоскости, обозначенные H и H’, каждая точка одной из которых отображается на другую с линейным увеличением +1.

Точка пересечения главных плоскостей с оптической осью называется главной точкой.

Главные плоскости НЕ совпадают с оптическими элементами системы.

Узловыми точками передней N и задней N’ осей называются две сопряжённые точки на оси, обладающие свойствами, что лучи проходящие через них являются параллельными.

Если оптическая система находится в однородной среде, то узловые точки совпадают с соответствующими главными точками, т.е. N-> H и N’->H’.

Задним фокусомрасстояния оптической системы будем называть расстояние от задней точки H’ до заднего фокуса F’ и обозначаем f’.

Передним фокусом расстояния будем называть передней точкой Hдо заданного фокуса F и обозначаем f.

При анализе оптической системы используют правила знаков.

-положительное направление луча – слева направо.

-расстояние, отсчитываемое от соответствующей координаты точек к лучу считается >0, против луча - <0.

Из рисунка f’>0, а f<0.

Если перед оптической системой есть среда с n, а после неё среда с n’, то можно доказать, что f/f’=-n/n’, т.е. в однородной среде f=-f’.

Ф=n’/f’=n/f – оптическая сила системы. Если Ф>0, то система собирающая, если Ф<0 – рассеивающая.

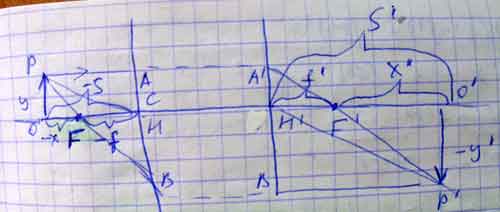
xx'=ff’ – уравнение Ньютона для оптической системы.

1/f’=1/S’-1/S => -1/S+1/S’=1/f’ – уравнение Гаусса (уравнение отрезка).

Тонкой линзой будем называть линзу, толщина которой во много раз меньше радиусов кривизны R₁ и R₂ её сферических поверхностей, т.е. d<<R₁ и d<<R₂.

Фокусное расстояние линзы 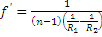, где n – показатель преломления материала линзы по отношению к среде, где она находится; R₁ и R₂ – радиусы кривизны 1-ой и 2-ой поверхности. При подстановке R надо использовать правило знаков: если центр кривизны справа (слева) от сферической поверхности, то R - “+” (R – “-“).