Стационарное уравнение Шредингера
Решение уравнения Шредингера представим в виде произведения двух функций, одна из которых есть функция только координат, другая функция только времени, причем зависимость от времени задается гармоническим множителем exp(-iωt) = exp(- i(W/ħ)t):
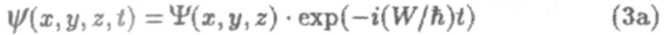
Здесь W — полная энергия частицы. Подставив (3а) в общее уравнение Шредингера и сократив на соответствующий экспоненциальный множитель, после небольших преобразований получим стационарное уравнение Шредингера:
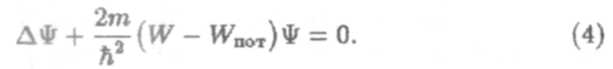
Покажем, как из уравнения Шредингера получается квантование энергии частицы, т.е. ситуация, с которой мы имеем дело, рассматривая атом водорода. Для наглядности математических выкладок выберем, однако, более простую модельную задачу, позволяющую понять, почему происходит квантование энергии.
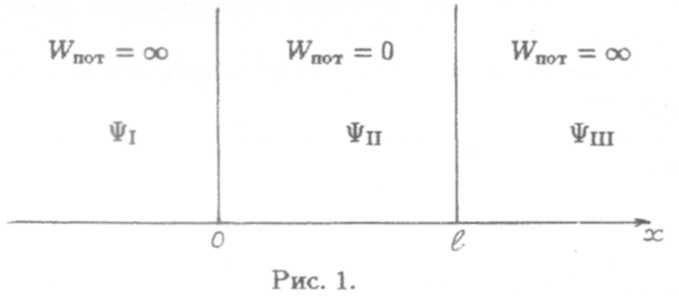
| Применим уравнение (4)к случаю, изображенному на рисунке. Тогда имеем ψI= ψIII = 0. Электрон в областях х <0 и х > lнаходиться не может. Этому препятствует бесконечно высокий |
Рассмотрим электрон в одномерной (д /ду = 0, д/дz = 0) бесконечно глубокой потенциальной яме размером l (рис. 1).
потенциальный барьер. Электрон находится где-то в промежутке 0 < х < l. Записывая уравнение (4) для области II, подучим
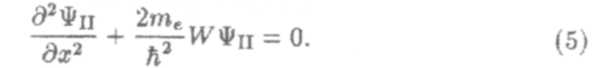
Общее решение уравнения (5), уравнения гармонических колебаний, можно записать в виде

Используя граничное условие при х = 0, найдем
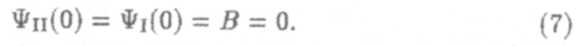
Второе граничное условие при х = l дает
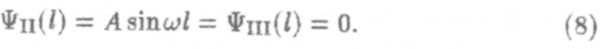
Так как А ≠ 0, то sinωl = 0. Это возможно только в том случае, когда ωl =nπ, п — целое, отсюда следует квантование величины ω, а значит, и квантование энергии
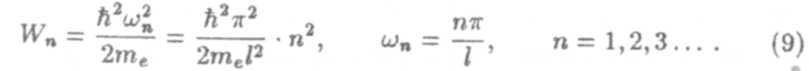
Энергия электрона может принимать только дискретные значения, так же как и в атоме водорода. Квантовые значения Wn называются уровнями энергии, а числа n, определяющие энергетические уровни частиц в потенциальной яме, называются квантовыми числами.
Подставив значения ωп в (6), получим
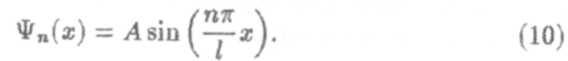
|
Используя условие нормировки, найдем
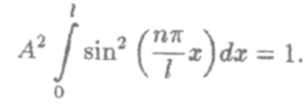
Отсюда после интегрирования имеем А = 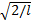 . Следовательно,
. Следовательно,
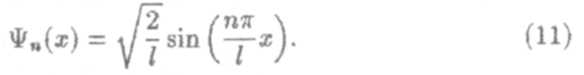
Положение электрона в пространстве точно определить невозможно. Понять это позволяют соотношения неопределенностей В.Гейзенберга, сформулированные им в 1927 году. Согласно этим соотношениям
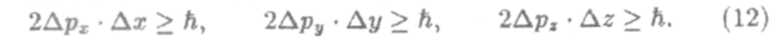
Здесь ∆px — неопределенность импульса частицы в направлении оси x,∆х — неопределенность координаты по этой же оси. Таким образом, чем точнее мы знаем положение частицы, тем более неопределенной оказывается ее скорость, и наоборот. Соотношения (12) вытекают из самой природы микрообъекта, являются его имманентными свойствами. Они никак не связаны с возможностями измерительных приборов.
Имеет место также еще одно соотношение, касающееся точности определения энергии микрообъекта. Оно имеет вид

где ∆W — неопределенность энергии микрообъекта, находящегося в данном состоянии, ∆t — время пребывания микрообъекта в этом состоянии. Значит, чем меньшее время микрообъект пребывает в каком-либо состоянии, тем более неопределенной становится его энергия в этом состоянии.
Уравнение Шредингера является мощным инструментом в исследовании физики микромира. С его помощью можно детально рассчитать атом водорода, а также более сложные многоэлектронные атомы и молекулы.
Соотношения неопределенностей позволяют нам понять, что микрообъект является достаточно сложным образованием, и описать некоторые из его свойств.
Лекция № 40
Дата добавления: 2015-08-11; просмотров: 859;
