Общее нерелятивистское уравнение Шредингера
Это уравнение играет в микропроцессах такую же фундаментальную роль, как законы Ньютона в классической механике. Шредингер ввел в аппарат физической теории новое понятие — волновую функцию ψ (x, y,z,t),Перечислим свойства этой функции.
1. Физический смысл этой функции заключается в том, что квадрат модуля волновой функции дает нам плотность вероятности обнаружить частицу в данной точке пространства:

где dp — вероятность обнаружить частицу в объеме dV.
2. Условие нормировки. Вероятность обнаружить частицу хотя бы в одной из точек бесконечного пространства, очевидно, равна единице. Математически это записывается в виде
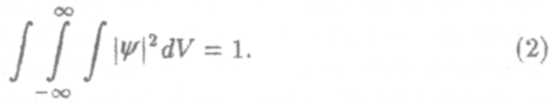
Здесь интегрирование ведется по объему всего бесконечного пространства.
3. ψ — однозначная, конечная и непрерывная функция своих аргументов.
4. Производные от ψ-функции по ее аргументам должны быть непрерывны.
В общем случае функция ψ удовлетворяет уравнению Шредингера
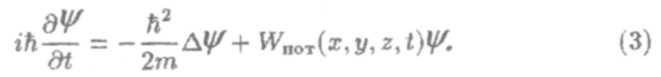
Здесь ∆ = д2/ дх2+ д2/ду2 + д2/ дz2 — оператор Лапласа, m — масса частицы, ħ = h/(2π), i — мнимая единица, Wnoт — потенциальная энергия частицы. Решая уравнение (3) и используя условия (1)-(4), можно с необходимой точностью определить значение волновой функции в любой точке пространства в данный момент времени.
Дата добавления: 2015-08-11; просмотров: 680;
