Принцип Гюйгенса-Френеля. Зоны Френеля

Дифракция света относится к явлениям, в которых проявля­ются волновые свойства света.

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонением от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми вол­нами препятствий и проникновению света в область геометриче­ской тени. Явление дифракции можно наблюдать, если разме­ры препятствий сравнимы с длиной волны, так как именно при этих условиях могут нарушаться законы геометрической опти­ки. Чем больше длина волны электромагнитного излучения, тем большую роль играют законы волновой оптики и тем более важ­ное значение приобретает дифракция волн.

Явление дифракции объясняется с помощью принципа Гюй­генса-Френеля, согласно которому каждая точка, до которой до­ходит волна, служит центром вторичных волн, а огибающая этих волн дает положение волнового фронта в следующий момент вре­мени (рис. 1).

Световая волна, распространяясь от источника, является ре­зультатом интерференции всех когерентных вторичных волн, воз­буждаемых волновой поверхностью. В случае падения плоской волны на преграду с отверстием, размеры которого сравнимы с длиной волны λ, наблюдается распространение волн в область геометрической тени (рис. 1).

Метод зон Френеля позволяет рассчитать амплитуду резуль­тирующего колебания в тех случаях, когда можно использовать соображения симметрии. Чтобы понять суть метода, разрабо­танного Френелем, надо определить амплитуду светового коле­бания, возбуждаемого в точке Р (рис. 2) сферической волной, распространяющейся от точечного источника S.

Волновые поверхности этой волны симметричны относитель­но прямой SP. Разобьем волновую поверхность на кольцевые зо­ны так, чтобы расстояния от краев каждой зоны до точки Р отли­чались от соседней зоны на λ/2. Колебания, приходящие от двух соседних зон в точку Р, находятся в противофазе (разность фаз колебаний от аналогичных точек соседних зон равна ж). Можно показать, что площадь зон примерно одинакова и равна

Расстояние от зоны до точки Р медленно растет с увеличением номера зоны т. Поэтому амплитуды колебаний, возбуждаемых в точке Р зонами Френеля, образуют монотонно убывающую по­следовательность

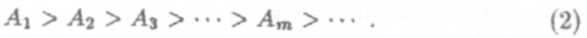
Фазы колебаний, возбуждаемых соседними зонами, отличаются на π. Результирующую амплитуду можно записать как

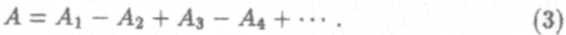
Это выражение можно представить как

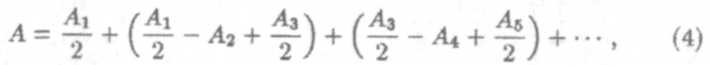
причем, в силу монотонного убывания амплитуды (2), можно при­ближенно считать, что

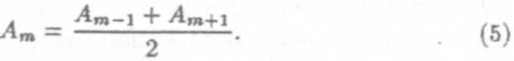
Если учесть, что число зон очень велико (при а = b = 0,1м и λ = 600 нм число зон превышает 6 • 10⁵) и амплитуда колеба­ний убывает с ростом номера m зоны, то согласно формуле (6), амплитуда А, создаваемая всей волновой поверхностью, равна половине амплитуды, создаваемой первой зоной:

Если на пути волны поставить экран с отверстием, открывающим только первую зону Френеля, амплитуда колебаний A₁ в два ра­за превысит амплитуду (6), а интенсивность увеличится в четыре раза. Если поставить на пути световой волны пластинку, которая перекрывает все четные (или нечетные) зоны, то интенсивность в точке Р (рис. 2) резко возрастет. Такая зонная пластинка дей­ствует подобно собирающей линзе. Результирующая амплитуда

А = A₁ + Аз + А₅ +^… оказывается во много раз больше, чем при

полностью открытом волновом фронте.