Дифракция Френеля. Рассмотрим дифракцию Френеля или дифракцию сферических волн от простейших преград.

Рассмотрим дифракцию Френеля или дифракцию сферических волн от простейших преград.

Если непрозрачный экран (рис. 3) с вырезанным в нем кру­глым отверстием открывает целое число m зон Френеля, то ре­зультирующая амплитуда в точке Р

где знак плюс соответствует нечетному числу зон Френеля, а ми­нус — четному. Следовательно, при нечетных т амплитуда в точке Р приближенно равна А₁ если число зон мало и в этой точке наблюдается максимум интенсивности I (рис. 3). При чет­ном числе зон А ≈ О, так как для малого отверстия А₁ ≈ А_т и наблюдается минимум интенсивности.

Если число зон велико, то А_т « А₁ и результирующая ам­плитуда А = А₁, т.е. дифракционная картина не наблюдается. При малом числе зон на экране (рис. 3) наблюдается дифракци­онная картина, имеющая вид чередующихся светлых и темных концентрических колец. На рис. 3 изображено распределение ин­тенсивности I (r) для случая m = 3, когда в центре, т.е. в точке Р, находится максимум интенсивности.

Если непрозрачный круглый диск закрывает m зон Френеля, то амплитуда в точке Р согласно (4):

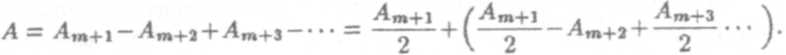
Выражение в скобках примерно равно нулю и

Можно показать, что дифракционная картина имеет вид череду­ющихся светлых и темных концентрических колец. В центре кар­тины расположено светлое пятно (пятно Пуассона), послужившее важным доказательством волновой природы света во время дис­куссии между сторонниками корпускулярной и волновой теории света в начале 19 века. Но наблюдение дифракционной картины возможно, если размеры диска соответствуют малому числу зон Френеля (при a = b=1м и λ = 500 нм радиус 4-ой зоны r₄ = 1 мм).