Наблюдение интерференции света
1. Опыт Юнга. Выясним, как выглядит интерференционная картина, создаваемая на экране двумя когерентными источниками монохроматического света S1 и S2. Расстояние от источников до экрана Э (рис .2) равно L, а расстояние между источниками — d, причем L » d.
Интенсивность в любой точке экрана Р определяется оптической разностью хода ∆l = |PS2| - |PS1|. Из рис.2 находим


откуда |РS2|2 - |PS1|2 = 2xd. Учитывая, что |РS2|2 - |PS1|2 ≈ 2L, имеем

Из условий максимумов и минимумов интерференции (6) и (7) получим координаты максимумов

и минимумов интерференционной картины

Число m является номером интерференционного максимума (минимума). Расстояние между соседними максимумами (минимумами), называемое шириной интерференционной полосы, равно

Интерференционная картина представляет собой чередование светлых и темных полос, параллельных друг другу. Интерференция света в тонких пленках. Пусть имеется плоскопараллельная прозрачная пленка с показателем преломления n2. Монохроматическая волна из среды с показателем преломления n1 падает на эту пленку под углом а (рис. 3).
В результате преломления и отражения возникают лучи 1 и 2, которые являются когерентными и дадут интерференционную
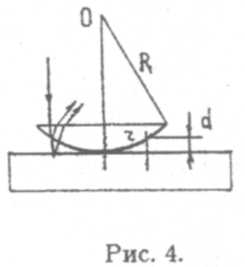
картину, определяющуюся оптической разностью хода ∆l между этими лучами
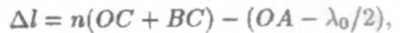
где член — λ0/2 обусловлен потерей полуволны при отражении света в точке О от оптически более плотной среды (n > 1).
Согласно рис. 3, ОС - С В = d/cos τ, OA - ОB sin а -2dtgτsin a. Учитывая закон преломления света sin a = n sin τ, получим
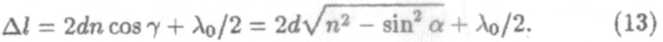
В точке P будет наблюдаться максимум или минимум интенсивности, если оптическая разность хода (13) будет удовлетворять условию (6) или (8). Случай интерференции света в тонких пленках является примером возникновения полос равного наклона, так как каждому наклону (a = const) лучей соответствует своя интерференционная полоса.
3. Кольца Ньютона. Интерференционная картина наблюдается в данном случае при отражении света, падающего на плоскую поверхность линзы от верхней и нижней поверхностей воздушного зазора между линзой и плоскопараллельной пластинкой. Интерференционные полосы, возникающие вследствие интерференции от мест одинаковой толщины, называются полосами равной толщины.
В данном случае они имеют вид концентрических окружностей. В отраженном свете оптическая разность хода с учетом потери полуволны при отражении ∆l = 2d+ λ0/2, где d — ширина воздушного зазора. Из рис. 4 следует, что R2 = (R — d)2 + r2, где r — радиус окружности, всем точкам которой соответствует одинаковый зазор d. Так как R2 = R2 - 2Rd + d2 + r2 и d « R,получим r2 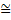 2Rd и
2Rd и
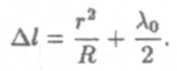
|
Приравняв (14) к условиям максимума (6) и минимума (8), получим выражение для радиуса m-го светлого кольца
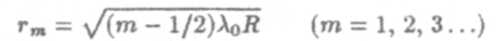
и радиуса m-го темного кольца
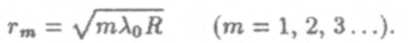
|
Дата добавления: 2015-08-11; просмотров: 872;
