Условия возникновения и сущность явления интерференции

В конце 19 века на основе накопленного экспериментального материала и развития представлений о свете возникли две тео­рии света: корпускулярная (И.Ньютон) и волновая (Х.Гюйгенс). К началу 19 века восторжествовала волновая теория. Большая заслуга в этом принадлежит английскому физику Т.Юнгу, иссле­довавшему явления интерференции и дифракции света, и фран­цузскому физику О.Френелю, дополнившему принцип Гюйгенса и объяснившему эти явления.

Создание Максвеллом в 70-х годах 19 века электромагнитной теории света, рассматривавшей свет как электромагнитные вол­ны с длиной волны от 0,38 мкм до 0,78 мкм, еще более упрочило позиции сторонников волновой теории света.

Интерференция света является одним из явлений, доказыва­ющих волновую природу света. Необходимым условием наблю­дения интерференции волн является их когерентность.

Волны называются когерентными, если они имеют одинако­вую частоту и разность их фаз остается постоянной во време­ни. Этому условию удовлетворяют монохроматические волны т.е. волны одной частоты. Обычные источники света не дают монохроматического излучения. Поэтому для наблюдения ин­терференции прибегают, как правило, к искусственному приему: раздваивают" свет, исходящий из одного источника.

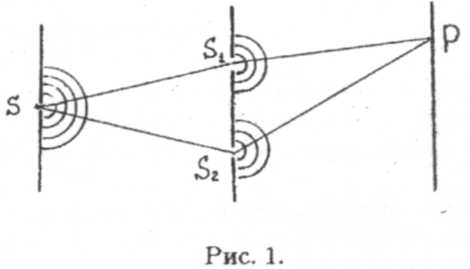
Первое наблюдение интерференции провел в 1802 году То­мас Юнг. Солнечные лучи пропускались через очень малое от­верстие в непрозрачном экране, после чего прошедшее излуче­ние расщеплялось на два пучка посредством установки второго экрана с двумя малыми отверстиями (рис. 1). Источник света S создает в отверстиях второго экрана вторичные источники S₁ и S₂, играющие роль когерентных источников.

Результат сложения колебаний, приходящих в Р (рис. 1) от двух когерентных источников S_t и S₂, будет зависеть от разности фаз этих колебаний. Предположим, что две монохроматические волны возбуждают в точке Р колебания одинакового направле­ния x₁ = A₁ sin(ωt + φ₁)и x₂ = A₂ sin (ωt + φ₁).Под x понимают

напряженность электрического Е или магнитного Н полей вол­ны: вектора Е и Нколеблются во взаимно перпендикулярных плоскостях. Амплитуда результирующего колебания в данной точке Р (см. лек. № 7)

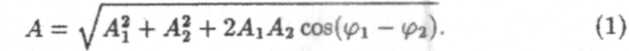
Интенсивность результирующей волны / пропорциональна ква­драту амплитуды колебаний, т.е. I ~ А². Напомним, что ин- . тенсивность показывает, какая энергия переносится за единицу у времени через единицу площади в направлении, перпендикуляр­ном направлению распространения волны. Большинство изме­рительных приборов, а также глаз человека оценивают энерге­тические характеристики световых волн, а не их амплитуду. Ин­тенсивность I результирующего колебания связана с интенсивностями I₁и I₂, созданными источниками S₁ и S₂, следующим образом:

Если источники S₁ и S₂ были некогерентными, то среднее значе­ние (cos(φ₂ — φ₁)) = 0 и I = I₁ +I₂ Но для когерентных источников разность фаз (φ₂ — φ₁)является постоянной во времени величи­ной, зависящей от положения точки Р. В тех точках простран­ства, где cos(φ₂ — φ₁) > 0, интенсивность I > I₁ +I_2. Наоборот, если cos(φ₂ — φ₁) <0, то I < I₁ +I₂

Интерференция света — это явление наложения когерентных волн, при котором происходит перераспределение интенсивности света в пространстве, в результате чего возникает чередование максимумов и минимумов интенсивности, называемое интерфе­ренционной картиной.

Если разность фаз колебаний, приходящих от источников S₁ и S₂, равна ∆φ=2πт, то I_max = I₁ +I₂ +2 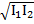и наблюдается интерференционный максимум (усиление света в данной точке).

Если разность фаз ∆φ = π(2т + 1), то I_min = I₁ +I₂ - 2 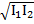и наблюдается интерференционный минимум, т.е. волны гасят друг друга.

При равенстве интенсивностей источников S₁ и S₂ (I₁= I₂ = I₀) максимум интерференции соответствует интенсивности I_max = 4 I₀, а минимум — I_min = 0. Для сравнения заметим, что для некогерентных источников интенсивность результирующей волны всюду одинакова и равна I= I₁ +I₂ = 2 I₀