Дифракция Фраунгофера
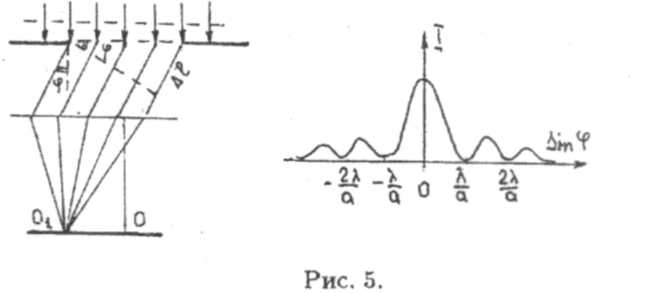
Дифракция Фраунгофера или дифракция в параллельных лучах наблюдается, если источник света находится далеко от экрана, либо если точечный источник поместить в фокусе собирающей линзы, установленной за препятствием (рис. 5)
1. Дифракция от одной щели. Рассмотрим дифракцию Фраунгофера от длинной щели (ширина щели а намного меньше ее длины). Пусть монохроматическая плоская волна распространяется в направлении, перпендикулярном плоскости щели и экрана (рис. 5). В точке О возникает максимум интенсивности, образованный лучами, распространяющимися в первоначальном направлении (в соответствии с законами геометрической оптики).
Для лучей, распространяющихся под углом φ к первоначальному направлению от крайних точек щели М и N, оптическая
разность хода составляет

Разобьем волновую поверхность MN на зоны Френеля. Ширина каждой зоны должна быть выбрана так, чтобы разность хода от ее краев составляла λ/2. Далее, используя метод зон Френеля (9), легко видеть, что при четном числе зон наблюдается дифракционный минимум в точке O1:
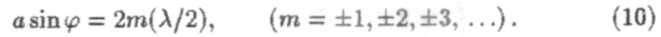
Если число зон Френеля нечетное, то наблюдается дифракционный максимум:
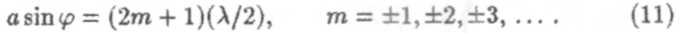
На рис. 5 приводится зависимость интенсивности I дифракционной картины от sin φ. Основная часть световой энергии сосредоточена в центральном максимуме (m = 0). При сужении щели центральный максимум становится шире и яркость его уменьшается. При а > λ A sin φ → 0, и имеет место прямолинейное распространение света.
2. Дифракционная решетка. Дифракционная решетка — это система из большого числа одинаковых щелей, разделенных одинаковыми непрозрачными промежутками. Дифракционная картина в этом случае определяется как результат интерференции волн, идущих от всех щелей, т.е. осуществляется многолучевая
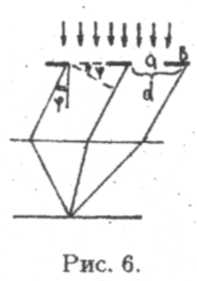
интерференция. Рассмотрим дифракционную решетку (рис. 6). Пусть ширина каждой щели а, а ширина непрозрачных промежутков b. Величина d = а+b называется постоянной (периодом) дифракционной решетки. Плоская монохроматическая волна падает нормально к плоскости решетки.
Разность хода лучей, идущих от двух соседних щелей (например, из точек М и N на рис. 6), равна

Если фазы колебаний в точках М и N совпадают (∆φ = 2π, ∆l = тλ), то действие одной щели усиливает действие другой щели в соответствии с условием интерференционных максимумов. Это дает условие главных максимумов дифракционной картины:
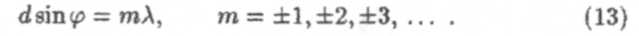
Кроме этого наблюдаются минимумы и максимумы (10,11), связанные с дифракцией от каждой щели в отдельности. Расчеты показывают, что если дифракционная решетка содержит N щелей, то условием главных минимумов является (см. (10))
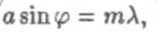

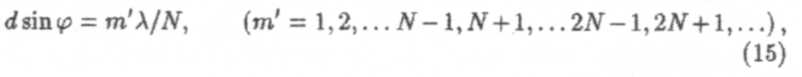
а условием дополнительных минимумов
где т’ принимает все целые значения, кроме О, N, 2N, 3N,..., так как при этих значениях выполняется условие (13). Между двумя главными максимумами располагаются N — 1 дополнительных минимумов.
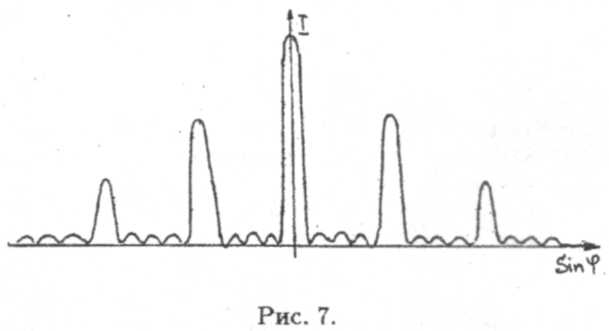
Положение главных максимумов зависит от длины волны λ (рис. 7), число т в (13) определяет номер дифракционного максимума, причем m ≤ d/λ, sinφ ≤1. При пропускании света, где присутствуют разные длины волн, все максимумы, кроме центрального, раскладываются в спектр. Поэтому дифракционные решетки используются для спектрального анализа (определения длин волн и интенсивности спектральных линий). Дифракционная решетка должна удовлетворять условию d ~ λ. Современные дифракционные решетки содержат около 2000 штрихов на 1 мм (d ≈ 0,5 мкм).
Дифракция света наблюдается на трехмерных (пространственных) решетках, в качестве которых могут служить кристаллы, а также в мутных (неоднородных) средах.
Явление дифракции определяет границы разрешающей способности оптических приборов. Изображение светящейся точки даже в случае идеальной оптической системы представляет дифракционную картину (чередование темных и светлых колец вокруг центрального светлого пятна).
Изображения двух одинаковых точечных источников согласно критерию Релея разрешимы, если центральный максимум дифракционной картины от одного источника совпадает с первым минимумом дифракции для второго источника (рис. 4). Соответствующий расчет для круглого отверстия дает, что первый минимум отстоит от центра дифракционной картины на угловое расстояние

где D — диаметр отверстия, B частности, D может являться диаметром объектива, и тогда условие (16) определяет разрешающую способность объектива

которая может быть увеличена только за счет уменьшения длины волны используемого излучения или за счет увеличения диаметра объектива D.
Разрешающая способность спектрального прибора R определяется величиной ∆λ минимальной разности длин волн спектральных линий (λ и λ + dλ), при которой эти линии регистрируется раздельно.

Для дифракционной решетки

где т — порядок дифракционного максимума, а N — полное число щелей решетки. Разрешающая способность дифракционных решеток может достигать величины порядка 105.
Лекция № 35
Дата добавления: 2015-08-11; просмотров: 2205;
