В замкнутом контуре алгебраическая сумма э.д.с. равна ал­гебраической сумме падений напряжений на элементах этого кон­тура

Как обходить контур, по часовой стрелке или против часовой стрелки, выбирается произвольно. Если при обходе мы идем от "-" источника к "+", данная э.д.с. берется в сумме со знаком "+", если наоборот, то со знаком "-". Падение напряжения берется со

знаком "+", если направление обхода совпадает с направлением тока, и со знаком "—", если не совпадает.

Для контура на рис. 4:

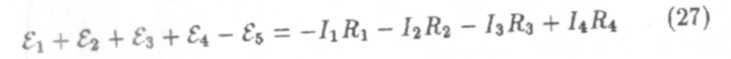
Число уравнений, составленных по второму правилу Кирхгофа, должно быть равно числу линейно независимых контуров в цепи. Линейно независимым называется такой контур, который содер­жит хотя бы один новый элемент по отношению к предыдущим.

Работаи мощность тока. Закон Джоуля ЛенцаРассмотрим мощность электрического тока, выделяемую в проводнике. При перемещении заряда dq в поле с разностью по­тенциалов U совершается работа

Отсюда мощность электрического тока:

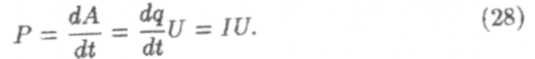
Используя закон Ома, ее можно выразить следующими форму­лами:

Совершаемая током работа идет на нагревание проводника, т.е. превращается в тепло. Механизмом этого превращения служат столкновения электронов с кристаллической решеткой. Соглас­но формулам (28) и (29), совершаемая током работа и, следова­тельно, выделяемое в проводнике за время t тепло

Это хорошо известный закон Джоуля-Ленца.

5. Закон Джоуля-Ленцав дифференциальной форме

Рассмотрим элемент проводника с поперечным сечением dS (рис. 1). Выделяемое в этом элементе за время dt тепло будет

Подставим в (31) значения I из (5) и R из (18); получится:

где dV = dS∙dl — объем рассматриваемого элемента проводника.

Количество тепла, выделяемое в единице объема за единицу времени, называется удельной тепловой мощностью w

Исходя из (32), получим формулу для удельной тепловой мощности элемента проводника:

Подставив в (34) значение плотности тока из (14) и принимая во внимание (15), получим:

Формула (35) — закон Джоуля-Ленца в дифференциальной фор­ме: удельная тепловая мощность тока равна произведению удель­ной электропроводности металла и квадрата напряженности электрического поля.

Лекция № 25