Контактная разность потенциалов

Получим формулу, позволяющую рассчитать величину кон­тактной разности потенциалов. Лля этого рассмотрим два вари­анта контактов. Пусть сперва контактируют два металла 1 и 2, у которых отличаются только работы выхода (рис. 1).

Пусть A₂ > А₁. Очевидно, что свободный электрон, попав­ший (в процессе теплового движения) на поверхность раздела металлов, будет втянут во второй металл, так как со стороны того металла на электрон действует большая сила притяжения (A₂ > А₁). Следовательно, через поверхность соприкосновения металлов происходит "перекачка" свободных электронов из пер­вого металла во второй, в результате чего первый металл заря­дится положительно, второй — отрицательно.

Возникающая при этом разность потенциалов φ’₁ — φ’₂ созда­ет электрическое поле напряженностью Е, которое затрудняет дальнейшую "перекачку" электронов и совсем прекратит ее, ко­гда работа перемещения электронов за счет контактной разности потенциалов станет равна разности работ выхода электрона из металла.

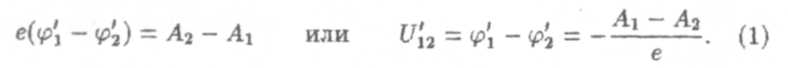
Во втором случае приведем в контакт два металла 1 и 2 с одина­ковыми работами выхода электронов, но с различными концен­трациями электронов п₁ и п₂ (рис. 2).

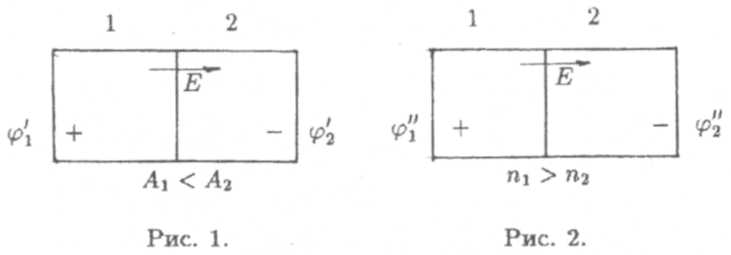
Пусть п₂ < п₁ .Тогда за счет диффузии начнется преимущественный перенос электронов из первого металла во второй. В результате первый металл зарядится положительно, второй - отрицательно. Возникающая при этом разность потенциале φ’’₁ — φ’’₂ между металлами создаст электрическое поле, которс затруднит дальнейшую "перекачку" электронов и, наконец, с всем остановит ее.

Получим формулу для контактной разности потенциалов, и пользуя классическую электронную теорию проводимости металлов. В этой теории утверждается, что свободные электроны в металле представляют собой "электронный газ", для которого справедливы законы идеального газа и который подчинятся законам статистики Максвелла-Больцмана. Тогда на основе классического распределения Больцмана для электронного газа можно написать:

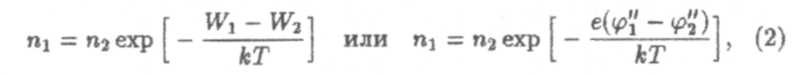
где W = εφ — потенциальная энергия электрона в металлах (не путать заряд электрона е и основание натуральных логарифмов). Прологарифмируем выражение (2)

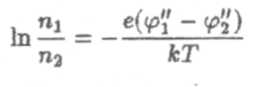
и получим формулу для контактной разности потенциалов

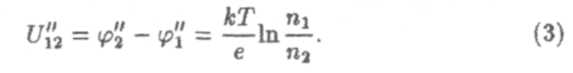
Если одновременно различны и работы выхода электронов из металла и концентрации электронов, то полная контактная раз­ность потенциалов

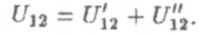
Используем выражения (1) и (3) и получим

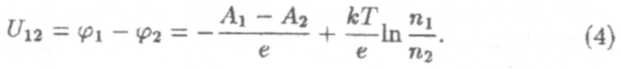
С помощью этой формулы можно качественно подтвердить пер­вый и второй законы Вольта.

Первый закон: работы выхода (A₁ и А₂) и концентрацииn₁ (n₁и n₂) являются характеристиками данных металлов, в формуле присутствует также температура (T).

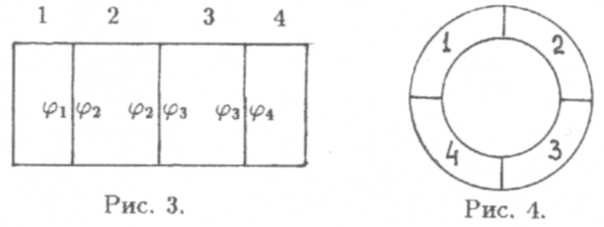
Для вывода второго закона Вольта составим цепь из несколь­ких (например, четырех) металлических проводников, соединен­ных (контактирующих) последовательно (рис. 3) и имеющих оди­наковую температуру. Очевидно, что разность потенциалов ме­жду концами этой цепи

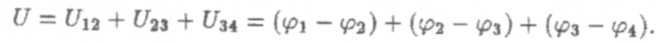
Раскроем скобки и получим U = φ₁ – φ₄ а следовательно,

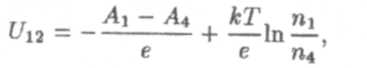
что является математическим выражением второго зако­на Вольта.

Важно отметить, что контактная разность потенциалов не создает электрического тока, так как потенциалы электронов, способных менять свое состояние, в точности равны.

Рассмотрим теперь замкнутую цепь, состоящую из несколь­ких разнородных проводников.

Например, соединим между собой концевые проводники 1 и 4 (рис. 4). Получим теперь результирующую разность потенци­алов

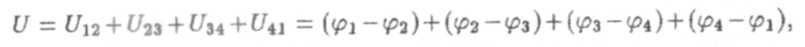
откуда очевидно получается U = 0, т.е.