Течение жидкости. Неразрывность струи

Жидкости, с которыми мы имеем дело в повседневной прак­тике, сжимаемы: их объем уменьшается а плотность растет с увеличением давления. Однако это уменьшение незначительно, то есть, реальные жидкости малосжимаемы; их сжимаемостью можно пренебречь.

В реальной движущейся жидкости действуют также силы внутреннего трения между слоями — жидкость вязка. Однако если указанные силы значительно меньше других сил, действу­ющих в задаче (например, силы тяжести), вязкость пренебре­жимо мала. Поэтому при упрощенном рассмотрении движения жидкости применяется модель идеальной жидкости:

Абсолютно несжимаемая и абсолютно невязкая жидкость назы­вается идеальной жидкостью.

При комнатной температуре модели идеальной жидкости неплохо соответствуют, например, спирт, эфир, вода.

Разобьем движущуюся жидкость на кусочки очень малых размеров — частицы жидкости или жидкие частицы. Каждой такой частице соответствует свой вектор скорости v.

Установившимся (стационарным) называется такое тече­ние жидкости, при котором жидкие частицы проходят через любую данную точку пространства с одной и той же скоростью.

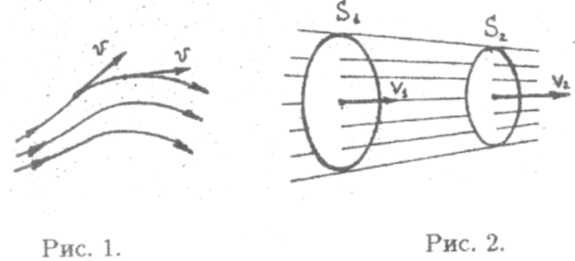
Проведем линии, направления касательных к которым в ка­ждой точке совпадают с направлениями скоростей жидких ча­стиц, находящихся в данный момент времени в этих точках (рис. 1). Такие линии называются линиями тока. Эти линии на­глядно изображают течение жидкости. Их принято проводить гуще в тех местах, где больше скорость течения.

При установившемся течении скорость жидкой частицы в любой момент времени полностью определяется ее положением. Частицы движутся вдоль линий тока, которые не изменяются со временем. Так как частица может иметь только одну траекто­рию, то две линии тока либо совпадают, либо вообще не имеют общих точек (не пересекаются).

Часть жидкости, ограниченная линиями тока, называется трубкой тока. Частицы жидкости перемещаются внутри своей трубки тока (рис. 2) как в трубе (отсюда и название), никогда не покидая ее. В самом деле, при выходе частицы за пределы трубки тока ее траектория (то есть, какая-то линия тока) пере­сечется с другой линией тока, ограничивающей данную трубку, что невозможно.

Выберем какие-нибудь два поперечных сечения с площадя­ми S₁ и S₂ некоторой достаточно узкой трубки тока идеальной жидкости (рис. 2). Так как трубка узкая, то можно считать, что все частицы сечения S₁движутся с одинаковой скоростью v₁, а сечения S₂— со скоростью v₂За малый промежуток времени ∆t через первое сечение протечет объем S₁v₁∆t, а через второе — S₂v₂∆t. Так как идеальная жидкость несжимаема и поток ее не разрывается, то эти объемы равны: S₁v₁= S₂v₂. Сечения были выбраны произвольно, поэтому:

Для данной трубки тока произведение площади поперечного се­чения трубки на скорость течения жидкости есть величина по­стоянная:

уравнение неразрывности струи. Оно справедливо также для ре­альных труб. Например, скорость течения реки увеличивается со сближением ее берегов.