Уравнение Бернулли

Выделим мысленно в наклонной трубке тока (или настоя­щей трубе) область, ограниченную сечениями S₁ и S_2,в кото­рых идеальная жидкость плотности р течет соответственно со скоростями v₁ и v₂ (рис. 2). За малое время ∆t масса жид­кости ∆m = pS₁v₁∆t втекает в указанную область, а масса ∆m = pS₂v₂∆t — вытекает оттуда. Эти массы равны в силу несжимаемости жидкости (плотность р постоянна) и уравнения неразрывности (1): ∆m₁ = ∆m₂ = ∆m.

Изменение полной энергии рассматриваемой области рав­но разности полных энергий втекающей и вытекающей масс: ∆W = W₂ — W₁. Поскольку же энергия каждой массы есть сумма ее кинетической и потенциальной энергий, то:

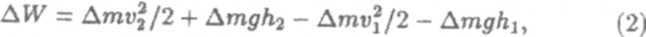
где g — ускорение свободного падения. Согласно закону со­хранения энергии, это изменение равно сумме работ внешних сил давления F₁ и F₂, действующих на соответствующие сече­ния (рис. 2): ∆W=∆A₁ + ∆А₂. Применяя определение работы, данное в разделе "Механика", получаем:

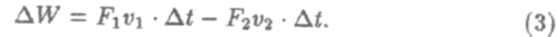
Если учесть, что F₁ = p₁ S₁ и F₂ = p₂S₂ (здесь p₁ и p₂ — давления в сечениях S₁ и S₁соответственно), то:

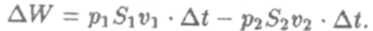
В то же время S₁v₁∆t = S₂v₂∆t = ∆V — протекший за время ∆t объем. Значит:

Теперь из формул (2-4) следует:

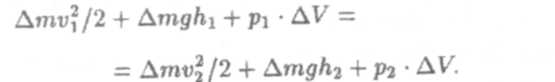
Разделим обе части последнего равенства на ∆V. С учетом того, что ∆m/∆V = р — плотность жидкости, это дает:

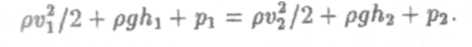
А поскольку сечения выбраны произвольно, получаем

Слагаемые в левой части (5) представляют собой, соответствен­но, кинетическую (pv²/2), потенциальную (pgh) и обусловленную силами давления (р) удельные (приходящиеся на единицу объ­ема) энергии жидкости. Таким образом, уравнение Бернулли(5) эквивалентно утверждению:

Для установившегося течения идеальной жидкости сумма удельных кинетической, потенциальной, и обусловленной силами давления энергий одинакова в любом поперечном сечении потока.

Эта формулировка логично следует из вывода уравнения Бер­нулли с использованием закона сохранения энергии, следствием которого оно и является. Слагаемым в левой части (5) можно приписать не только смысл удельных энергий, но и давлений. Относительно упругого давления р и гидростатического pgh это очевидно. Первое слагаемое pv²/2 также имеет размерность да­вления и называется динамическим давлением. Поэтому урав­нение Бернулли можно трактовать и так:

Для установившегося течения идеальной жидкости полное да­вление, равное сумме динамического, гидростатического и упру­гого давлений, одинаково в любом поперечном сечении потока.

Если трубка тока горизонтальна (pgh = const), то уравнение Бернулли принимает вид:

т.е. чем больше скорость, тем меньше статическое давление. Это утверждение иллюстрируется установкой, изображенной на рис. 3. Поскольку, согласно уравнению неразрывности, ско­рость течения больше на более узких участках трубы, показа­ние манометров (измеряющих статическое давление) на этих участках меньше: если S₁ < S₂ < S₃, то p₁ < p₂ < p₃.

A.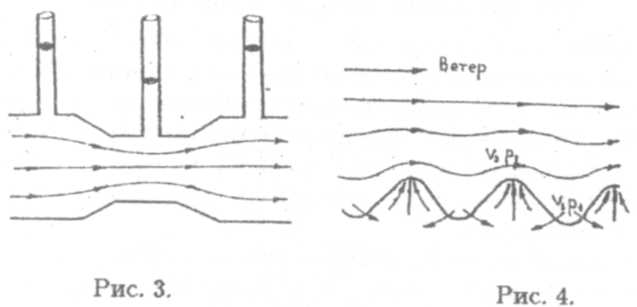

Рассмотрим вспаханное поле, где валы чередуются с бо­роздами (рис. 4). Пусть ветер дует перпендикулярно направле­нию борозд. Тогда приземный слой воздуха можно рассматри­вать как трубку тока с переменным сечением (над бороздами сечение максимально, а над валами — минимально). Исходя из вышеизложенного, давление над бороздами больше, чем над валами. Поэтому в поверхностном слое почвы возникает дви­жение воздуха, направленное от оснований борозд к вершинам валов. Так происходит газообмен между почвой и атмосферой. Это явление носит название аэрации почвы.

Лекция № 19