Капиллярные явления

Пусть капля жидкости лежит на поверхности твердого тела (см. рис. 3). Возможно два варианта:

А. Молекулы жидкости сильнее притягиваются к молекулам твердого тела, нем к друг к другу. Жидкость стремится уве­личить площадь соприкосновения с поверхностью, растекаясь по ней (рис. 3а). Краевой угол  между поверхностями капли и поверхности — острый (< 90°). В этом случае говорят, что жидкость смачивает твердое тело. Если  = 0°, то имеет место полное смачивание. Например, вода смачивает стекло, а ртуть — медь.

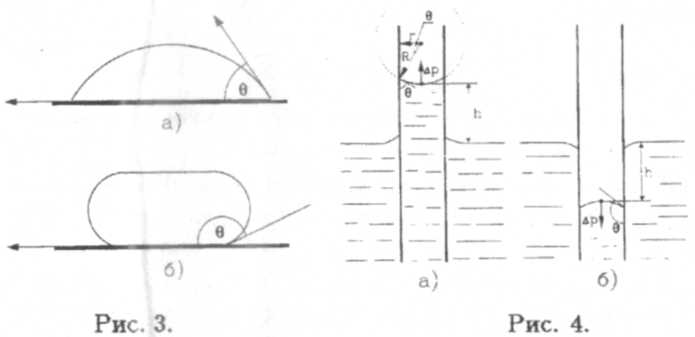
Б. Молекулы жидкости сильнее притягиваются друг к другу, чем к молекулам твердого тела. Жидкость стремится умень­шить площадь соприкосновения с поверхностью, принимая фор­му сплюснутого (силой тяжести) шара (рис. 36);  > 90°. Теперь жидкость не смачивает твердое тело, а при  = 180° получаем полное несмачивание. Примеры: вода и воск, ртуть и стекло.

В силу изложенного, края жидкости в сосуде из смачивае­мого ей материала приподнимаются (рис. 4а), а из несмачиваемого — опускаются (рис. 4б). Заметим, что на рис. 4 изобра­жены очень узкие сосуды — капилляры; только их мы и будем рассматривать (в обычном сосуде отмеченные краевые эффекты малозаметны). Поверхность жидкости в капилляре имеет вогну­тую (смачивание) или выпуклую (несмачивание) сферическую (капилляр считаем цилиндрическим) поверхность — мениск.

Мениск стремится выпрямиться, что вызывает избыточное давление ∆р, направленное к центру кривизны (рис. 4а и 4б).

Величина избыточного давления ∆р под сферической поверхно­стью жидкости радиуса R равна (Лаплас, 1805):

где а — коэффициент поверхностного натяжения жидкости, при­чем знак “-’’ в (4) соответствует вогнутому, a “+” — выпуклому мениску.

Поэтому в случае смачивания жидкость в капилляре подни­мается на высоту h_, так что давление столба жидкости этой высоты уравновешивает избыточное давление: pgh s= Др, где р — плотность жидкости, a g 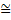9.81 м/с² — ускорение свободного падения на поверхности Земли. Учитывая (4), получаем:

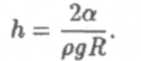
Радиус капилляра r, мениска R и краевой угол  связаны соотношением (рис. 4а): R = r/ cos. Получаем окончательно:

Высота поднятия смачивающей жидкости в капилляре обратно пропорциональна его радиусу (Борелли, 1670 и Жюрен, 1718).

Формула (5) носит название формулы Борелли-Жюрена, а ве­личина 2а/рg в квадратных скобках — капиллярной постоянной. Очевидно, что жидкость, которая не смачивает стенки капил­ляра, опускается в нем на величину, даваемую формулой (5).

Благодаря капиллярам, образованным клетками растений происходит их питание: вода с растворенными в ней питатель­ными веществами поднимается по этим капиллярам до самых верхушек деревьев. Мельчайшие зазоры между комочками поч­вы также образуют капиллярную систему, от функционирования которой зависит влажность верхнего почвенного слоя.

Лекция № 17