Спільне використання методів HMQC/HMBC для віднесення сигналів 13С
Розглянемо, як гетероядерну кореляційну спектроскопію можна використати для віднесення сигналів у вуглецевому спектрі нескладної органічної сполуки, що має будову:
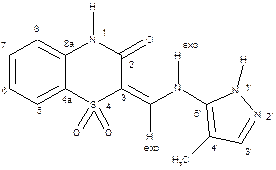
6.12.
Перш за все, вимірюються протонний та вуглецевий спектри сполуки. Вони слугуватимуть для позиціювання кроспіків у двомірних спектрах. Після цього проводять віднесення сигналів у протонному спектрі. Якщо сигнали спостерігаються окремо, то зробити це вдається, базуючись на їхній мультиплетності та положенні в спектрі. У більш складних випадках слід долучити до цього вивчення спектри COSY. Фрагменти протонного та вуглецевого спектрів, що містять сигнали ароматичних протонів та атомів вуглецю наведено на осях двомірних спектрів на Рис. 6.49 та 6.50. Після віднесення протонних сигналів можна вимірювати та обробляти спектри HMQC та НМВС. Нижче наведено ці спектри для сполуки 6.12.
 |
Рис. 6.49. Спектр HMQC сполуки 6.12. Для збільшення масштабу спектру сигнал метильної групи не показаний.
 |
Рис. 6.50. Спектр НМВС сполуки 6.12. У спектрі присутня невелика домішка диметилформаміду з сигналами при 2,7 та 2,9 м.ч.
Обробка гетероядерних кореляційних спектрів полягає у визначенні координат кроспіків у мільйонних частках. На наведених рисунках всі кореляції для кожного з протонних сигналів містяться на горизонтальній лінії, що проведена на двомірному спектрі через відповідний протонний сигнал. В спектрі HMQC кожному протонному сигналу відповідає лише одна кореляція, оскільки протон має зв’язок лише з одним вуглецевим атомом. На відміну від цього, кількість кореляцій, що відповідають кожному з протонних сигналів в спектрі НМВС може бути достатньо великою, залежно від того, скільки вуглецевих атомів відокремлені від протона на 2-3 хімічних зв’язки. При аналізі складних спектрів для виявлення координат всіх кореляцій буває необхідним записати окремо кілька фрагментів двомірного спектру у потрібному масштабі. Результати такої обробки зручно представляти у вигляді таблиці
Таблиця 6.8. Гетероядерні кореляції, знайдені для сполуки 6.12.
| d, м.д. | HMQC | HMBC |
| 12,38 | - | 148,6; 141,2; 94,6 |
| 11,10 | - | 148,6; 101,0 |
| 11,01 | - | 163,3; 136,0; 126,3; 118,4; 101,0 |
| 8,39 | 145,5 | 163,3; 148,6; 101,0 |
| 7,76 | 122,0 | 136,0; 134,2 |
| 7,58 | 134,2 | 136,0; 126,3; 122,0; 118,4 |
| 7,25 | 123,5; 118,4 | 136,0; 134,2; 126,3; 123,5; 122,0; 118,4 |
| 6,12 | 94,6 | 148,6; 141,2 |
| 2,18 | 11,4 | 148,6; 141,2; 94,6 |
Дані, що зведені у таку таблицю, аналізувати набагато простіше, ніж ті, що є у самому двомірному спектрі, хоча, звісно, вони є ідентичними. Відсутність кореляції HMQC для якогось протонного сигналу свідчить про те, що даний протон сполучений не з атомом вуглецю. Таку ситуацію ми бачимо в Табл. 6.8 для сигналів протонів NH в області 11-12,5 м.ч. Найбільш зручно проводити віднесення сигналів, якщо накреслити структурну формулу сполуки і поступово записувати біля магнітних ядер величини хімічних зсувів, що їм відповідають, дістаючи їх з отриманих кореляцій. Перш за все, відносять протоновані атоми вуглецю, оскільки зробити це набагато легше. Після цього починають віднесення четвертинних атомів вуглецю. Найважливіші кореляції НМВС доцільно показувати викривленими стрілками. Починати віднесення слід з сигналів, що відповідають найбільш простим структурним фрагментам. Так, базуючись на віднесеному сигналі протона 1NH можна знайти хімічні зсуви близьких до нього четвертинних атомів С2, С3, С4а, С8а. На початку аналізу отримані у такий спосіб величини хімічних зсувів не слід вважати кінцевими, оскільки треба, щоб знайдені віднесення узгоджувались зі всіма знайденими кореляціями. Результат віднесення для сполуки 6.12 наведено на схемі. Тут кореляції HMQC не показані, а стрілками позначено лише кореляції НМВС, що послужили основою для віднесення сигналів четвертинних атомів вуглецю
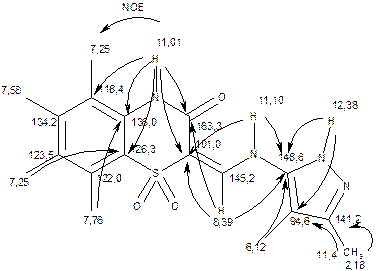
Рис. 6.51. Віднесення сигналів та схема найважливіших НМВС-кореляцій для сполуки 6.12.
Даний результат аналізу гетероядерних кореляцій можна без особливих змін використовувати для публікацій у спеціальній літературі, або будувати на його базі відповідні таблиці. Часто віднесення сигналів можна перевірити альтернативним методом, наприклад, за допомогою ЯЕО.
Дата добавления: 2015-08-11; просмотров: 659;
