Визначення міжспінових відстаней

Очевидно, найбільш важливим «стороннім» впливом на релаксацію спіна I у багатоспіновій системі є вплив ядер, відмінних від S. Диполярна взаємодія із цими спінами приводить до прискорення поздовжньої релаксації спінів I незалежно від процесів крос-релаксації між I і S. Тому ЯЕО між I і S слабшає. Для ілюстрації впливу сусіднього спіна розглянемо гіпотетичну трьохядерну спінову систему, що містить ядра I, S і N (сусіднє ядро). Нехай релаксація відбувається винятково за диполь-дипольним механізмом, а всі інші механізми релаксації відсутні (Рис. 1.56).

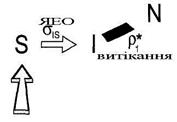
Рис.1.56.Трьохспінова система в якій сусіда I-спіна, N, діє як зовнішнє джерело релаксації для спіна I через їхню взаємну диполярну взаємодію

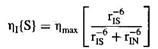
Якщо припустити для простоти, що ЯЕО існує тільки між ядрами I і S, для стаціонарного ЯЕО можна записати рівняння:

(1.40)

де h_max відповідає максимально можливому ЯЕО у двохспіновій системі. Відзначте, що за відсутності спіна N, ЯЕО просто дорівнює h_max і не має залежності від між’ядерних відстаней. Ефект введення додаткового спіна полягає у виникненні залежності ЯЕО від міжспінових відстаней. Однак величина ЯЕО не залежить просто від r^-6_IS. Вона визначається співвідношенням відстаней r_IS і r_IN. Це справедливо для всіх експериментів стаціонарного ЯЕО. Спостережувані величини ЯЕО завжди визначаються співвідношенням відстаней r_IS і всіх інших відстаней r_IN. У реальній молекулі сусідів може бути досить багато і всі вони впливають на ЯЕО ядра I. Таким чином, величина стаціонарного ЯЕО ядра I визначається відношенням швидкостей крос-релаксації між ядрами I і S і сумарною швидкістю релаксації спіна I на всіх інших ядрах. Рівняння 1.40 показує також, що зменшення між’ядерної відстані між I і S приводить до збільшення ЯЕО між спінами I і S, оскільки внесок крос-релаксації в загальну релаксацію при цьому зростає. Таким чином, у багатоспіновій системі малі міжспінові відстані відповідають великим величинам ЯЕО.

Однак, як показано на Рис. 1.57, дане правило слід застосовувати з певною обережністю. Нижче представлені величини ЯЕО h_B{A} для трьохспінової системи А-В-С, у якій відстань між спінами В і С змінюється. При цьому безпосередньою взаємодією між спінами А і С будемо нехтувати. Коли С перебуває далеко від В, його вплив на релаксацію спіна А виявляється малим. Тому крос-релаксація між А і В домінує і ЯЕО виявляється близьким до максимально можливого. Якщо А і С перебувають від В на рівних відстанях, то вони відіграють однакову роль у релаксації В, тому для ЯЕО одержимо половину максимальної величини. Якщо ж С перебуває набагато ближче до В, ніж А, то домінуючою є релаксація В на ядрах С, а крос-релаксація відносно неї виявляється слабкішою. Тому в цьому випадку ЯЕО буде маленьким.

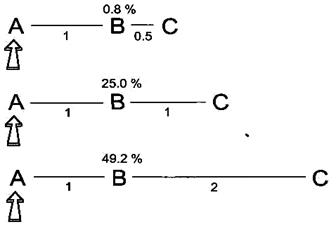
Рис. 1.57. Розраховані стаціонарні ЯЕО A => B для ізольованої трьохспінової системи із близькими між’ядерними відстанями. Стрілка показує спін, що насичується. Пряма взаємодія A-C ігнорується.

Таким чином, якщо два спіни перебувають поблизу один до одного і між ними є сильна диполярна взаємодія, то ЯЕО між ними може бути і маленьким, якщо неподалік розташовується третій спін.

Ще одну цікаву особливість можна виявити, якщо в описаній вище трьохспіновій системі насичувати ядро В і визначати ЯЕО для ядра А, тобто знаходити h_А{В} (Рис. 1.58). Видно, що в цьому випадку ЯЕО для А лише в невеликому ступені залежить від відстані між В і С. Це пов'язане з тим, що ядро С виявляє слабкий вплив на релаксацію ядра А, внаслідок чого процес крос-релаксації між ядрами А і В у всіх випадках домінує. Таким чином, ЯЕО виявляються несиметричними, тобто h_B{A} не дорівнює h_А{В}, оскільки хімічне оточення ядер А і В істотно розрізняється.

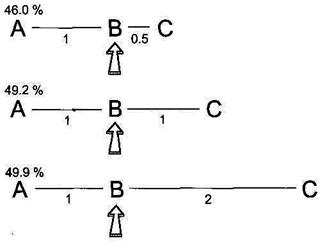
Рис. 1.58.Розраховані стаціонарні ЯЕО В => А для ізольованої трьохспінової системи із близькими між’ядерними відстанями. Стрілка показує спін, що насичується. Пряма взаємодія A-C ігнорується.