Принцип управления по хранимой программе
Напомним, что функция микропрограммного управляющего автомата определяется:
- множеством входных сигналов (логических условий): Х = {х1, х2 …х n };
- множеством выходных сигналов (микрокоманд): У = {у1, у2 …у k };
- микропрограммой (ГСА), задающей порядок следования выходных сигналов У в зависимости от значений входных сигналов X.
Если автомат Мура описан прямой таблицей переходов, то для каждого состояния am известно:
- множество выходных сигналов У(am), вырабатываемых автоматом в состоянии am;
- множество входных сигналов Х(am), определяющих все возможные переходы автомата из состояния am в состояние as;
- множество состояний as, в которые может перейти автомат из состояния am (обозначим A(am).
Для каждого состояния автомата Мура (а значит для каждой операторной вершины ГСА) эту информацию, необходимую и достаточную для описания закона функционирования автомата, можно закодировать и представить двоичным словом (микрокомандой – не путать с выходным сигналом автомата уi, который часто так же называют микрокомандой !), которое имеет следующую структуру:
| № | уm1 | уm2 | … | уmk | хm1 | хm2 | … | хmn | аm1 | аm2 | … | аms |
где:
№ – номер двоичного слова, соответствующего состоянию автомата аm (или его адрес ЗУ, где будет храниться микропрограмма);
уmi – выходной сигнал (микрокоманда), который должен вырабатывать автомат в данном состоянии аm; в общем случае таких сигналов k; эта часть двоичного слова называется операционной;
хmi – входной сигнал (логическое условие), участвующее хотя бы в одном переходе из am в as ; в общем случае таких сигналов n; эта часть двоичного слова называется управляющей;
аmi – одно из состояний аs , в которое может перейти автомат из состояния аm при определенных значениях логических условий хmi. Поскольку описание одного состояния – это одно двоичное слово, имеющее свой адрес в ЗУ, аmi можно считать адресом состояния аmi в ЗУ; в общем случае таких состояний s. Если количество логических условий в слове равно n, то количество аmi равно 2 в степени n. Эта часть двоичного слова называется адресной.
Воспользуемся прямой таблицей переходов автомата Мура из примера (п.3.1).
| № | a m | a s | Y as | Xa ma s |
| a 0 | a 0 a 1 | y7 y1, y2 | Ø x 3 x 3 | |
| a 1 | a 2 a 3 | y3 y4, y5 | x 1 Ø x 1 | |
| a 2 | a 3 | y4, y5 | ||
| a 3 | a 4 a 0 | y6 y7 | Ø x 2 x 2 | |
| a 4 | a 2 a 3 | y3 y4, y5 | x 1 Ø x 1 |
Если использовать приведенную выше структуру двоичного слова, то для описания данного автомата достаточно пяти двоичных слов (по числу состояний автомата), имеющих следующий формат:
| № | уm1 | уm2 | хm | ах=0 | ах=1 |
Сам номер (№) в слово помещать не нужно, так как это адрес слова в ЗУ. В слове под уmi отведено два поля, так как максимальное количество уmi в состоянии аm равно двум; под хmi – достаточно отвести одно поле, так как в любом переходе из аm в аmi (или аs) участвует только одно логическое условие. Под аmi достаточно отвести 2 поля: для адреса перехода при хm = 0 (ах=0) и при хm = 1 (ах=1). Используя выбранный формат двоичного слова можно составить в виде таблицы содержательную микропрограмму, описывающую работу автомата.
| № | уm1 | уm2 | хm | ах=0 | ах=1 | a m |
| у7 | - | х3 | a 0 | |||
| у1 | у2 | х1 | a 1 | |||
| у3 | - | х3 | a 2 | |||
| у4 | у5 | х2 | a 3 | |||
| у6 | - | х1 | a 4 |
В этой таблице – каждая строка соответствует одному из состояний автомата (столбец am); № - соответствует адресу слова, описывающего это состояние в ЗУ. В колонках уm1 и уm2 записаны микрокоманды, вырабатываемые автоматом в состоянии am, в колонке хm записаны логические условия, определяющие переходы из состояния am в состояния, адреса которых в ЗУ записаны в колонках ах=0 и ах=1, в колонке a m записаны пояснения: какому состоянию автомата соответствует данная строка.
Каждая из колонок этой таблицы (кроме am) должна быть представлена двоичными кодами. Количество двоичных разрядов для каждой колонки можно выбрать таким:
- уm1 – 3 разряда: здесь будем записывать номер уm1 (от 1 до 7);
- уm2 – 3 разряда: здесь будем записывать номер уm2 (от 1 до 7);
- хm – 2 разряда: здесь будем записывать номер хm (от 1 до 3);
- ах=0 – 3 разряда: здесь будем записывать адрес ах=0, по которому в автомате должен произойти переход к следующему слову при хm =0 (от 0 до 4);
- ах=1 – 3 разряда: здесь будем записывать адрес ах=1, по которому в автомате должен произойти переход к следующему слову при хm =1(от 0 до 4).
Таким образом разрядность двоичного слова в нашем примере равна 14. Закодированная микропрограмма имеет вид, приведенный в таблице. В каждой колонке записаны двоичные числа в соответствии с принятыми выше соглашениями. Требуемый объем памяти – 70 бит. Рассмотрим подробнее 2-ю строку в этих таблицах.
| № | уm1 | уm2 | хm | ах=0 | ах=1 |
В этой и предыдущей таблицах в строке №2 описывается состояние автомата a2. Из этого состояния – безусловный переход автомата в состояние a 3. Поэтому в столбце хm может быть записан номер любой переменной хm , а в обоих столбцах ах=0 и ах=1 одинаковый адрес перехода. Так как записанный в столбце хm обязательно имеет одно из значений: 0 или 1, то переход будет безусловным по адресу ах=0 = ах=1.
Схема, обеспечивающая работу с закодированной микропрограммой, должна содержать следующие функциональные узлы:
- память для хранения микропрограммы (ЗУ) объемом не менее пяти слов; чтение слова из памяти осуществляется по адресу, подаваемому на адресный вход ЗУ; разрядность слов – 14 бит;
- схему, преобразующую двоичный код уm1 и уm2 в унитарный код, соответствующий закодированному уi; эта схема – дешифратор (DCу);
- мультиплексор (MSх), выбирающий из множества входных сигналов Х всего один, номер которого записан в столбце хm;
- мультиплексор (MSа), выбирающий из слова адрес ах=0 (если выбранное мультиплексором MSх значение хm=0) или адрес ах=1 (если выбранное мультиплексором MSх значение хm=1);
- регистр адреса (RG), в который необходимо по импульсу синхронизации записать выбранный мультиплексором MSа адрес и подать его на адресный вход ЗУ, из которого будет считано следующее слово (иначе – переход в следующее состояние).
| уm1 | уm2 | хm | ах=0 | ах=1 |
Пронумеруем разряды двоичного слова с 1 по 14 (как показано в таблице); номера разрядов будут соответствовать номерам выходов ЗУ.
Функциональная схема автомата приведена на рис.27.
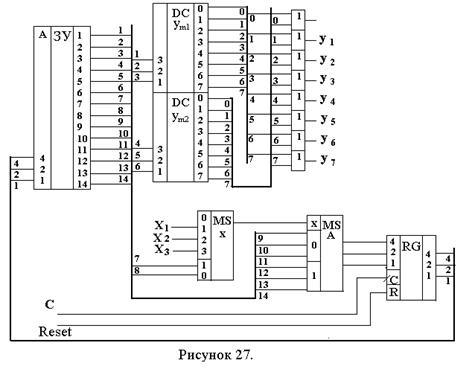
На этой схеме кроме описанных выше элементов имеется 8 дизъюнкторов, объединяющих одноименные выходы дешифраторов DCуm1 и DCуm2 . Эти элементы необходимы в случае, если одна и та же микрокоманда уi будет записана в разных строках микропрограммы в разных столбцах уm1 и уm2.
Автомат (рис.27) работает следующим образом. Сигнал Reset=1 устанавливает значение «0» во всех разрядах регистра RG. Код (или двоичное число) А=000 с выхода RG подается на адресный вход ЗУ. На выходах ЗУ (разряды 1..14) появляется слово, записанное по адресу 0 (см. таблицу). В этом слове:
разряды 1,2,3 – подаются на вход DCуm1 и, поскольку в этих разрядах записано число 111 (7), на выходе «7» DCуm1 формируется 1, а значит и выходной сигнал у7 = 1;
разряды 4,5,6 – подаются на вход DCуm2 и, поскольку в этих разрядах записано число 000 (0), (которое мы не использовали для кодирования уi) на выходе «0» DCуm1 формируется «1», но ни на каких либо других выходах уi эта «1» не появится;
разряды 7,8 – подаются на управляющие входы мультиплексора MSх; в этих разрядах записано число 11 (3). Значение логического условия х3 появляется на выход MSх;
мультиплексор MSа, в зависимости от значения х3 («0» или «1») подает на входы регистра адреса RG либо адрес перехода, записанный в разрядах 9,10,11 (если х3 = 0), либо адрес перехода, записанный в разрядах 12,13,14 (если х3 = 1);
при поступлении на вход С импульса синхронизации, этот адрес запишется в регистр RG и с его выходов поступит на адресный вход ЗУ, на выходе которого появится слово, записанное по этому адресу.
Таким образом за один цикл (время между синхроимпульсами С) автомат считает из ЗУ некоторое двоичное слово, выработает микрокоманды уm, проанализирует входные сигналы хm, и в зависимости от их значения выберет адрес следующего двоичного слова в ЗУ.
Спроектированный нами интуитивно автомат содержит много избыточности и был приведен в качестве примера, как естественное воплощение наших рассуждений. Недостатками такого подхода являются, прежде всего, сложность схемы (при достаточно простых функциях автомата) и не оптимальная длина микрокоманды (двоичного слова), что приводит к неэффективному использованию памяти ЗУ.
Рассмотрим некоторые приемы, позволяющие сделать автомат с программируемой логикой более оптимальным, чем приведенный на рис.27.
Дата добавления: 2015-08-11; просмотров: 1027;
