Принудительная адресация микрокоманд в автомате.
В начале раздела на рис.27 и 28 приведены схемы автомата с принудительной адресацией. В отличие от естественной, принудительная адресация сводится к указанию в каждом слове адреса (или адресов) следующего слова. Однако даже при двухадресной микрокоманде, когда в каждом двоичном слове всего одно логическое условие, длина адресной части может быть значительной. Есть различные способы уменьшения длины адресной части в двоичном слове. Один из них заключается в следующем. В адресной части слова записывают адрес перехода при Xi = 0 (Адр хi=0), а если X i = 1, то адрес перехода Адр вычисляется так:
| № | a m | a s | Y as | Xa ma s |
| a 0 | a 0 a 1 | y7 y1, y2 | Ø x 3 x 3 | |
| a 1 | a 2 a 3 | y3 y4, y5 | x 1 Ø x 1 | |
| a 2 | a 3 | y4, y5 | ||
| a 3 | a 4 a 0 | y6 y7 | Ø x 2 x 2 | |
| a 4 | a 2 a 3 | y3 y4, y5 | x 1 Ø x 1 |
Адр = Адрхi=0 + 1.
Если использовать логическое значение переменной Xi как арифметическое (0 или 1), то адрес перехода можно вычислить так:
Адр = Адрхi=0 + Xi.
Таким образом, сократив вдвое длину адресной части двоичного слова, мы не потеряли возможность осуществлять условный переход в автомате с естественной адресацией. Однако при этом получили некоторое неудобство: двоичные слова, к которым происходит переход, всегда находятся в ЗУ в соседних ячейках, так как адреса у них различаются всегда на 1. Поэтому в микропрограмме автомата с описанным способом адресации может появиться избыточность в виде дублирования некоторых слов и безусловных переходов.
Воспользуемся ГСА (рис.5), прямой таблицей переходов автомата Мура из примера в п.3.1. и форматом микрокоманды из первого примера текущего раздела, в котором в адресной части оставим только одно поле ах=0.
| К(Уi) | хm | ах=0 | |||||
Используем кодирование наборов микрокоманд и дополнительное ЗУ (смотри рис. 29). Микропрограмма с комментариями приведена ниже.
У0 = {у7}; У1 = {у1, у2 }; У2 = {у3}; У3 = {у4, у5}; У4 = {у6};
К(У0) = 000; К(У1) = 001; К(У2) = 010; К(У3) = 011; К(У4) = 100.
Для организации безусловного перехода в этом примере введено дополнительное логическое условие X0 . В схеме автомата на вход X0 подадим значение «0», а значит переход в этом случае будет всегда по адресу ах=0, записанному в микрокоманде.
| Адрес | Комментарий \ разряды | ||||||||
| a 0; IF X3 = 0 THEN GOTO 0; | |||||||||
| a 1; IF ØX1 = 0 THEN GOTO 2; | |||||||||
| a 2; IF X0 =0 THEN GOTO 3; | |||||||||
| a 3; IF X 2 = 0 THEN GOTO 4; | |||||||||
| a 4; IF ØX1 = 0 THEN GOTO 2; | |||||||||
| a 0; IF X3 = 0 THEN GOTO 0; |
Из таблицы видно, что на состояние a 0 пришлось использовать два слова в ЗУ, тем не менее, общий объем ЗУ в нашем примере 48 бит (меньше, чем у двухадресной микрокоманды).
Функциональная схема автомата приведена на рис.31.
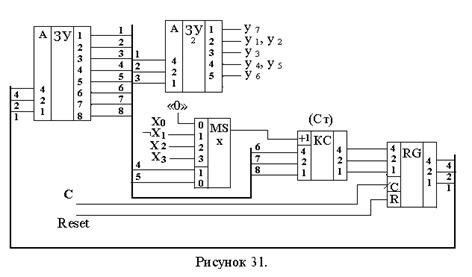
Отличие этой схемы от рис.28 состоит в использовании вместо мультиплексора адреса MSа комбинационного счетчика (Ст). Комбинационная схема (КС), обозначенная как Ст, выполняет функцию: Ст:=А + Xi, где:
Ст – двоичное число на выходе КС;
А – адрес перехода при Xi= 0;
Xi – значение логического условия Xi, выбранного мультиплексором MSх в соответствии с кодом, записанным в разрядах 4 и 5 микрокоманды и интерпретируемым как число 0 или 1.
Функционирование схемы (рис.31) практически не отличается от описанной выше схемы на рис.28.
Используя описанный выше прием формирования адресов переходов, можно еще на один разряд сократить адресную часть микрокоманды. Так как адреса переходов всегда отличаются на 1, то в качестве младшего разряда адреса очередной микрокоманды можно использовать значение логического условия Xi. Формат микрокоманды в этом случае имеет вид, приведенный в таблице. Старшие разряды адресной части (аС) записаны в микрокоманде, а младший разряд формируется из значения логического условия Xi.
| К(Уi) | хm | аС | Xi | ||||
| Адрес | Комментарий \ разряды | ||||||||
| a 0; IF X3 = 0 THEN GOTO 0; | X3 | ||||||||
| a 1; IF ØX1 = 0 THEN GOTO 2; | ØX1 | ||||||||
| a 2; IF X0 =0 THEN GOTO 6; | X0 | ||||||||
| a 3; IF X 2 = 0 THEN GOTO 4; | X 2 | ||||||||
| a 4; IF ØX1 = 0 THEN GOTO 2; | ØX1 | ||||||||
| a 0; IF X3 = 0 THEN GOTO 0; | X3 | ||||||||
| a 3; IF X 2 = 0 THEN GOTO 4; | X 2 | ||||||||
 В следующей таблице приведена микропрограмма (на основе предыдущего примера), в которой функцию младшего разряда адреса перехода выполняет соответствующее логическое условие Xi, а на рис. 32 – функциональная схема автомата.
В следующей таблице приведена микропрограмма (на основе предыдущего примера), в которой функцию младшего разряда адреса перехода выполняет соответствующее логическое условие Xi, а на рис. 32 – функциональная схема автомата.
Схема не содержит комбинационного счетчика КС, однако такой формат микрокоманды накладывает на микропрограмму ограничение: при Xi=0 – адрес перехода всегда четный, а при Xi=1 –всегда нечетный.
| А\биты ЗУ2 | (у7) | (у1,у2) | (у3) | (у4,у5) | (у6) |
Таблица для ЗУ 2
Дата добавления: 2015-08-11; просмотров: 2311;
