Лекция 15.
Тема 8.2. Структурный синтез МПА Мура на ПЛМ. Вопросы оптимизации МПА
Простейшая матричная реализация автомата Мура
Рассмотрим реализацию автомата Мура на ПЛМ на примере из п. 3.1.1. Отличие в синтезе автомата Мура на ПЛМ состоит только на этапе построения обратной структурной таблицы и функциональной схемы автомата.
Возьмем за основу структурную таблицу автомата Мура на жесткой логике из п. 3.1.1. Будем использовать в качестве элементов памяти состояний D-триггеры. Добавим в таблицу еще один столбец Тamas, в который будем записывать функции переходов: Тamas = am Ù Xamas (табл. 3.14).
В схеме автомата Мура используются следующие матрицы:
М&(1) («И1») – для вычисления функций переходов Тamas ;
М1(1) («ИЛИ(1)») – для вычисления функций управления элементами памяти D2 , D1 и D0;
М&(2) («И2») – дешифратор состояний; так как в автомате Мура yi зависит только от состояния as, функции переходов Тamas нельзя использовать для вычисления yi;
М1(2) («ИЛИ(2)») – для вычисления функций yi как дизъюнкция выходных сигналов (переменных as) с матрицы М&2.
Таблица 3.14
| № п/п | am | Kam | as | Kas | Xamas | Yas | Famas | Тamas |
| a 0 a 3 | a 0 | Ø x 3 x 2 | Y7 | D 2 D 2 | Т1= Q2ØQ1ØQ0Øx3 Т2= ØQ2ØQ1ØQ0 x2 | |||
| a 0 | a 1 | x 3 | y1, y2 | D 0 | Т3= Q2ØQ1ØQ0 x3 | |||
| a 1 a 4 | a 2 | x 1 x 1 | Y3 | D 1 D 1 | Т4= ØQ2ØQ1 Q0 x1 Т5= ØQ2 Q1 Q0 x1 | |||
| a 1 a 2 a 4 | a 3 | Ø x 1 Ø x 1 | y4, y5 | - - - | Т6= ØQ2ØQ1Q0 Øx1 Т7= ØQ2 Q1ØQ0 Т8= ØQ2 Q1 Q0 Øx1 | |||
| a 3 | a 4 | Ø x 2 | y6 | D1 ,D0 | Т9 =ØQ2ØQ1ØQ0Øx2 |
Функции D2, D1, D0 для нашего примера находятся как дизъюнкции соответствующих функций переходов Тamas, а yi зависят только от состояний автомата as:
D2 = T1 Ú T2; D1 = T4 Ú T5 Ú T9 ; D0 = T3 Ú T9 ;
y1 = y2 = a1. y3 = a2. y4 = y5 = a3. y6 = a4. y7 = a0.
Структурная схема автомата Мура на матрицах (простейшая реализация) имеет вид, показанный на рис. 3.35.
Матрицы М&(1) и М1(1) выполняют только функцию вычисления Famas. Матрица М&(2) на входе имеет коды состояний автомата Q2Q1Q0, а на выходе формирует значения переменных a0, a1 и т.д., соответствующих состояниям автомата. Матрица М1(2) используется для реализации функций выходов yi в случае, если они выражены через дизъюнкции ai.

Рис. 3.35
Функциональная схема автомата приведена на рис. 3.36. Для упрощения схемы в ней не показаны элементы, используемые для установки автомата в начальное состояние.
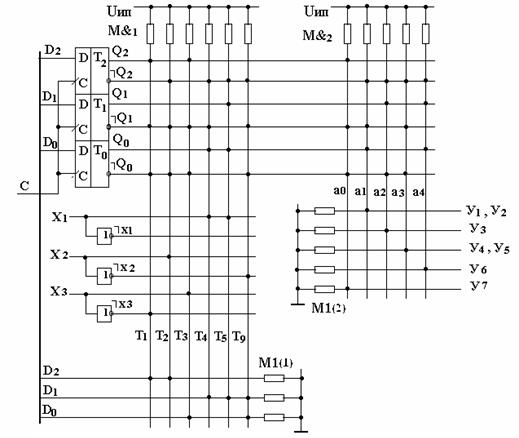
Рис. 3.36. Функциональная схема автомата
Как видно из схемы, матрицу М1(2) можно было не использовать, так как в нашем примере каждая функция yi зависит только от одной переменной ai.
3.3.4. Вопросы оптимизации автоматов на матрицах
Методы оптимизации автоматов на матрицах направлены, в основном, на сокращение суммарной площади матриц. Как было указано в п. 3.3.1, матрицы М& и М1 при тривиальной реализации автомата сильно разрежены: большая часть площади этих матриц не используется, так как в узлах нет диодов. Это касается части матрицы М&, вычисляющей функции переходов (в области переменных Х), и матрицы М1 (в области переменных У).
Кодирование логических условий Х. Площадь матрицы М& в автоматах Мили и Мура зависит:
1) от количества элементов памяти (количество выходов Q и ØQ элементов памяти обозначим КQ; КQ входит в общее число горизонтальных шин матрицы М&; КQ >= 2 • ] log2 | A | [ );
2) от количества переменных Х (количество горизонтальных шин от этих переменных КХ = 2•|Х| также входит в общее число горизонтальных шин матрицы М&);
3) от числа переходов Т(am as) автомата КТ.
Уменьшить КQ невозможно, так как в автоматах на матрицах используется всегда минимальное кодирование состояний. Количество переходов можно иногда уменьшить за счет использования разметки ГСА с узлами. В то же время в каждой конкретной функции переходов Тamas обычно используются не все переменные из множества Х, а только некоторые из них. Например, по структурной таблице из п. 3.3.2 и 3.3.3 видно, что в каждой функции Тamas используется максимум одна переменная Х (при общем их количестве 3), поэтому есть возможность уменьшить площадь SМ&за счет замены трех переменных Х одним логическим условием Р, принимающим значение определенной переменной Х в зависимости от состояния автомата am.
Алгоритм такой замены описан ниже.
1. Разобьем множество входных сигналов автомата (логических условий) Х на пересекающиеся подмножества Хам; элементами Хам являются логические условия Хj, определяющие все переходы автомата из состояния ам.
2. Найдем максимум a=max½Хам½ и введем новое множество, содержащее a логических условий Р={Р1, Р2...Рa}.
3. Каждую переменную хÎХам заменим на переменную из множества Р; составим таблицу этой подстановки. Желательно, чтобы одноименные логические условия Хj оказались в одном и том же столбце таблицы.
4. Запишем функции Рi= F(ам,xi), используя таблицу подстановки.
5. Закодируем состояния автомата таким образом, чтобы можно было реализовать эти функции на матрицах М& и М1 с минимальными затратами. Полученные коды состояний будем использовать далее при составлении структурной таблицы автомата.
6. Используем сформированные функции Рi вместо переменных Х в матрице М& для вычисления функций переходов автомата Тamas.
Например, пусть по размеченному графу автомата с шестью состояниями a0…a5 и семью логическими условиями х0…х6 получили следующие подмножества Хам:
Ха0={х0,х1}; Ха3={х5};
Ха1={х2,х3}; Ха4={х1,х3};
Ха2={х3,х4}; Ха5={х6}.
Нетрудно заметить, что Max ½Хаi½= 2.
Введем два новых логических условия: Р={Р1, Р2} и составим таблицу замены переменных Х на переменные Р.
| ам | Р1 | Р2 |
| а0 | х0 | х1 |
| а1 | х3 | х2 |
| а2 | х3 | х4 |
| а3 | х5 | - |
| а4 | х3 | х1 |
| а5 | х6 | - |
Запишем выражение для Р1 и Р2 :
Р1 = а0х0 Ú ( а1Ú а2Ú а4) х3 Ú а3х5 Ú а5х6
Р2 = а1х2 Ú ( а0Ú а4) х1Ú а2х4.
В этих выражениях, например, Р1 принимает значение логического условия х0, если автомат находится в состоянии а0 (так как при этом а0=1); значение х3, если автомат находится в одном из состояний: а1 или а2 или а4 и т.п.
Закодируем состояния автомата таким образом, чтобы выражения в скобках можно было записать в виде одного терма, используя переменные Q3, Q2, Q1 – сигналы с выходов элементов памяти состояний автомата. Используем карту Карно. В ячейках карты расставим состояния аI таким образом, чтобы была возможность осуществить их минимальное покрытие согласно скобочным частям выражений Р1 и Р2. Получим следующие коды состояний:
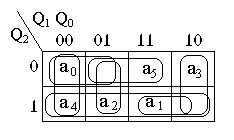
Ка0 = 000; Ка3 = 000;
Ка1 = 111; Ка4 = 100;
Ка2 = 101; Ка5 = 011.
Учитывая то, что в карте Карно есть свободные клетки, используем их для минимизации выражений Р1 и Р2 :
Р1 = а0х0 Ú ( а1Ú а2Ú а4) х3 Ú а3х5 Ú а5х6=
= ØQ2ØQ1 х0 Ú Q2 х3 Ú Q1ØQ0 х5 Ú ØQ2 Q0 х6 = Z1 Ú Z2 Ú Z3 Ú Z4 ,
где Z1= ØQ2ØQ1 х0 ; Z2 = Q2 х3; Z3 = Q1ØQ0 х5; Z4 = ØQ2 Q0 х6;
Р2 = а1х2 Ú ( а0Ú а4) х1Ú а2х4 =
= Q2 Q1 х2 Ú ØQ1ØQ0 х1ÚØQ1 Q0 х4 = Z5 Ú Z6 Ú Z7 ,
где Z5 = Q2 • Q1 • х2 ; Z6 = ØQ1•ØQ0• х1; Z7 = ØQ1• Q0•х4.

Рис. 3.37
Функциональная схема, реализующая преобразование логических условий Х в логические условия Р, приведена на рис. 3.37. Матрица М& вычисляет термы Z1 … Z7 , матрица М1 – функции Р1 и Р2.
Площадь матрицы М& равна
SМ&= (КХ + КQ) • КZ ,
где КХ – количество логических условий Х, в нашем примере – КХ=7; КQ – количество прямых и инверсных выходов элементов памяти, в нашем примере КQ = 6; КZ – количество термов в функциях Р1и Р2 , в нашем примере КZ=7.
Таким образом, в нашем примере SМ&=91.
Площадь матрицы М1 равна SМ1=КZ •КР , где КР – количество логических условий Р.
В нашем примере SМ1=14. Общая площадь матриц М& и М1, используемых для минимизации количества логических условий, равна
SМр= (КХ + КQ) • КZ + КZ •КР = (КХ + КQ +КР)* КZ .
Если не использовать кодирование логических условий Х, то площадь части матрицыМ&, вычисляющей функции переходов Тamas (в нашем примере этой матрицы нет) и использующей в качестве переменных Х, равна
SМТх=2 • КХ • КТ,
где КТ – количество переходов (строк) в структурной таблице автомата.
При замене логических условий Х на Р эта площадь составит
SМТр=2 • КР • КТ.
В итоге, при кодировании логических условий Х, площадь матриц, зависящая от Х, равна
SХр = SМр+SМТр= (КХ + КQ +КР)* КZ +2 • КР • КТ,
а без кодирования
SХх = SМТх=2 • КХ • КТ.
Использование описанного преобразования имеет смысл, если SХр заметно меньше, чем SХх. Разница в площадях матриц без кодирования и с кодированием логических условий
D SХ = SХх – SХр = 2 • КХ • КТ – (КХ + КQ + КР)•КZ – 2•КР•КТ =
= 2 • КТ • ( КХ – КР) – (КХ + КQ + КР)•КZ .
Чтобы эта разница была положительной (D SХ > 0), необходимо выполнение условия
2 • КТ • ( КХ – КР) > (КХ + КQ + КР)•КZ ,
иначе преобразование логических условий имеет смысл, если выполняется соотношение
КТ > ((КХ + КQ + КР)•КZ) / (2 • ( КХ – КР)).
Если условие выполняется и при этом DSХ имеет значительную величину (относительно SХх), то можно проделать описанную процедуру и получить при этом более эффективное использование матриц.
В нашем примере
D SХ =2 • КТ • ( КХ – КР) – (КХ + КQ + КР)•КZ .=
= 2 • КТ • ( 7 – 2) – (7 + 6 + 2) • 7 = 10 • КТ – 105.
Из полученных выражений видно, что D SХ > 0, если в автомате КТ>11 (количество переходов больше 11); при выполнении этого условия имеет смысл выполнить преобразование логических условий Х в логические условия Р.
Кодирование выходных сигналов автомата (микрокоманд yj ).В автоматах Мили при простейшей реализации (п. 3.2) в матрице М1 есть сильно разреженная часть, где вычисляются yi. Это происходит потому, что общее число микрокоманд в автомате может быть большим, но на каждом переходе вырабатывается небольшое число микрокоманд. В таком случае можно повысить эффективность использования матрицы М1, используя кодирование микрокоманд. Для этого необходимо:
1) выписать из ГСА или обратной структурной таблицы одинаковые группы микрокоманд, которые обозначить как Вi;
2) записать выражения для yi как ÈВj – дизъюнкция групп Вi, в которых функция yi =1;
3) составить граф отношений между группами Вi. Вершины графа соответствуют группам микрокоманд Вi, ребрами соединяются вершины (Вi.), содержащие одинаковые микрокоманды;
4) закодировать вершины (Вi) двоичным кодом (b1 b2 b3 …) таким образом, чтобы связанные вершины на графе можно было выразить через конъюнкцию переменных bi. Количество переменных bi должно быть минимальным и равно ] log2| B | [;
5) записать выражения для bj как ÈТj: где ÈТj – дизъюнкция функций переходов автомата Мили, на которых bj =1;
6) записать выражения yi=ÈВj через конъюнкцию переменных bi: уi=Çbj;
7) реализовать функции bj = ÈТj с помощью матрицы М1;
8) реализовать функции уi=Çbj с помощью матрицы М&.
Рассмотрим пример.
Таблица 3.15
| № | Y(amas) | Т(amas) | Вi | b1b2b3b4 |
| y1, y2 | T1 | B1 | 0 0 1 1 | |
| y1, y3 | T2 | B2 | 0 1 1 0 | |
| y7, y8 | T3 | B3 | 1 0 0 1 | |
| y1, y10 | T4 | B4 | 0 1 1 1 | |
| y5, y6 | T5 | B5 | 1 0 1 1 | |
| y3 | T6 | B6 | 1 1 1 0 | |
| y4, y8 | T7 | B7 | 1 1 0 0 | |
| y4, y8, y9 | T8 | B8 | 1 1 0 1 | |
| y1, y10 | T9 | B4 | 0 1 1 1 | |
| y4, y8 | T10 | B7 | 1 1 0 0 | |
| y4, y8, y9 | T11 | B8 | 1 1 0 1 | |
| y1, y10 | T12 | B4 | 0 1 1 1 | |
| y5, y6 | T13 | B5 | 1 0 1 1 | |
| y5, y6 | T14 | B5 | 1 0 1 1 | |
| y4, y8, y9 | T15 | B8 | 1 1 0 1 | |
| y1, y10 | T16 | B4 | 0 1 1 1 | |
| y7, y8 | T17 | B3 | 1 0 0 1 | |
| y9 | T18 | B9 | 0 1 0 1 | |
| y5, y11 | T19 | B10 | 1 0 1 0 |
Допустим имеется обратная структурная таблица (табл. 3.15) автомата Мили для реализации на ПЛМ, из которой мы выпишем только столбец Yamas, а в столбце Тamas оставим только обозначение функций переходов Тi. Остальные столбцы таблицы нас не интересуют. Из этой таблицы видно, что площадь матрицы М1 при простейшей реализации автомата, использующаяся для формирования микрокоманд yi, равна
SМУ=КУ • КТ = 11• 19 = 209.
В этом примере количество микрокоманд, которые может формировать автомат, равно 11 (y1…y11), но на каждом из 19 возможных переходов T1 … T19 формируется максимум 3 микрокоманды.
Добавим в эту таблицу еще два столбца. Первый – для обозначения групп микрокоманд (Вi); в нашем примере – 10 различных групп микрокоманд (обозначим их B1...B10). Во втором столбце будем записывать коды групп Вi. Минимальное количество разрядов для кодирования Вi равно четырем. Обозначим код Вi: b1 b2 b3 b4.
Выразим yi через дизъюнкцию Вj, в которые входит yi:
y1 = B1 Ú B2 Ú B4 ;
y2 = B1 ;
y3 = B2 Ú B6 ;
y4 = B7 Ú B8;
y5 = B5 Ú B10;
y6 = B5;
y7 = B3;
y8 = B3 Ú B7 Ú B8;
y9 = B8 Ú B9;
y10 = B4;
y11 = B10.
Используя выражения yi=ÈВj построим граф отношений между группами Вi, в котором ребрами соединяются вершины (Вi.), содержащие одинаковые микрокоманды (рис. 3.38). Используя карту Карно, закодируем группы Вi так, чтобы можно было совместно покрыть связанные вершины (смотри карту Карно).
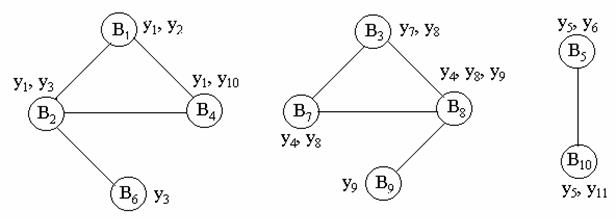
Рис. 3.38
По карте Карно запишем коды Bi (КBi), выраженные через значения переменных b1 b2 b3 b4:

КВ1=0011; КВ2=0110; КВ3=1001;
КВ4=0111; КВ5=1011; КВ6=1110;
КВ7=1100; КВ8=1101; КВ9=0101;
КВ10=1010.
Запишем полученные коды групп микрокоманд в столбец (b1b2b3b4) структурной таблицы автомата и выразим функции bi как дизъюнкцию соответствующих переменных Ti той же таблицы:
b1 = T3Ú T5Ú T6Ú T7Ú T8Ú T10Ú T11Ú T13Ú T14Ú T15Ú T17Ú T19 ;
b2 = T2Ú T4Ú T6Ú T7ÚT8ÚT9Ú T10Ú T11Ú T12Ú T15Ú T16Ú T18 ;
b3 = T1Ú T2Ú T4Ú T5Ú T6Ú T9Ú T12Ú T13Ú T14Ú T16Ú T19 ;
b4 = T1Ú T3 Ú T4Ú T5Ú T8Ú T9Ú T11Ú T12Ú T13Ú T14Ú T15Ú T16Ú T17 Ú T18.
Выразим yi , записанные через дизъюнкцию Вj, в виде конъюнкции уi=Çbj (согласно покрытиям в карте Карно):
| y1 = B1 Ú B2 Ú B4 = Øb1 b3; | y2 = B1 = Øb1 Øb2 ; |
| y3 = B2 Ú B6 = b2 b3 Øb4 ; | y4 = B7 Ú B8= b1 b2 Øb3 ; |
| y5 = B5 Ú B10 = b1 Øb2 b3 ; y7 = B3 = b1 Øb2 Øb3 ; y9 = B8 Ú B9 = b2 Øb3 b4 ; y11 = B10 = b1 Øb2 b3 Øb4 ; | y6 = B5 = b1 Øb2 b3 b4 ; y8 = B3 Ú B7 Ú B8 = b1 Øb3 ; y10 = B4 = Øb1 b2 b3 b4 . |
Реализуем функции b1 … b4 с помощью матрицы М1, а функции y1 … y11 – с помощью матрицы М& (рис. 3.39).
Оценим суммарную площадь матриц М1 иМ& , реализующих функции выходов автомата Мили с кодированием микрокоманд:
SМb=Кb • КТ = 4 • 19 = 76, где КТ – количество переменных, используемых для кодирования групп микрокоманд; SМУb=2 • Кb • КУ = 2 • 4 • 11 = 88; SМУк = SМb + SМУb = 76 + 88 = 164.
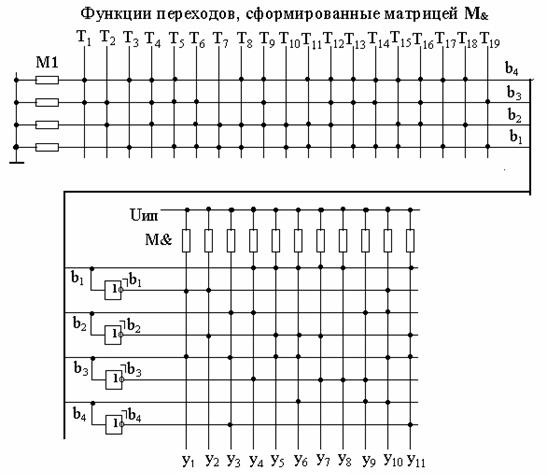
Рис. 3.39
Разница в площадях матриц без кодирования и с кодированием составляет
D SУ = SМУ – SМУк= 209 – 164 = 45.
Экономия площади матриц позволяет реализовать более сложный автомат на меньшей площади кристалла матрицы.
Кодирование микрокоманд имеет смысл производить, если выполняется условие
КТ • (КУ – Кb ) > 2 • Кb • КУ .
Решение о кодировании можно принять после определения количества групп микрокоманд Вj и возможности их минимального кодирования переменными bj.
На рисунках приведены обобщенные структурные схемы автомата Мили с кодированием логических условий и микрокоманд (рис. 3.40) и автомата Мура с кодированием логических условий и микрокоманд (рис. 3.41).
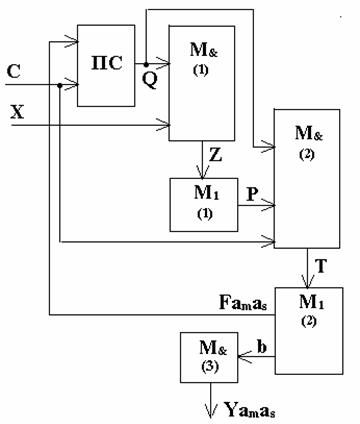
Рис. 3.40
В схеме автомата Мили используются следующие элементы:
– память состояний – ПС;
– матрица М&(1), вычисляющая термы zi для последующего вычисления логических условий Р матрицей М1(1);
– матрица М&(2), вычисляющая функции переходов Тi;
– матрица М1(2), вычисляющая функции управления элементами памяти состояний Famas и коды групп микрокоманд КВi (b1b2...);
– матрица М&(3), вычисляющая значения функций yi.
В схеме автомата Мура используются следующие элементы:
– память состояний – ПС;
– матрица М&(1), вычисляющая термы zi для последующего вычисления логических условий Р матрицей М1(1);
– матрица М&(2), вычисляющая функции переходов Тi;
– матрица М1(2), вычисляющая функции управления элементами памяти состояний Famas;
– матрица М&(3), выполняющая функции дешифратора состояний автомата и вычисляющая значения функций аi;
– матрица М1(3), вычисляющая значения функций yi.
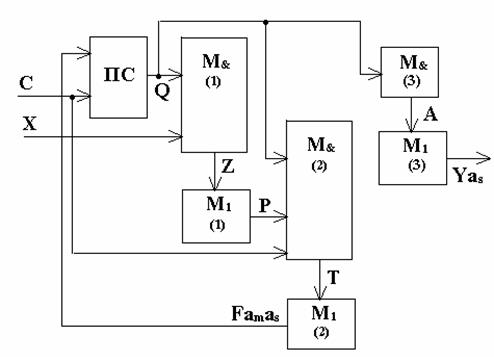
Рис. 3.41
Дата добавления: 2015-08-11; просмотров: 1058;
