Лекция 14.
Раздел 8. Синтез цифровых автоматов на программируемых матрицах (ПЛМ)
Тема 8.1. Структурный синтез МПА Мили на ПЛМ. Вопросы оптимизации МПА
Матричная реализация комбинационных схем (КС)
На этапе логического проектирования сложных цифровых устройств управления большие трудности возникают из-за их нерегулярности и малой повторяемости отдельных узлов. В п. 3.1 были рассмотрены методы синтеза управляющих автоматов с жесткой логикой. «Жесткость» заключается в том, что любое изменение в алгоритме работы автомата приводит к изменению в комбинационных схемах, реализующих функции переходов и выходов автомата.
Существуют регулярные, настраиваемые пользователем структуры, называемые программируемыми логическими матрицами (ПЛМ). ПЛМ содержат в себе две матрицы – матрицу «И» (М&) и матрицу «ИЛИ» (М1), соединенные последовательно. Матрица «И» вычисляет конъюнкцию логических переменных, а матрица «ИЛИ» – дизъюнкцию полученных термов. Таким образом, пару матриц «И» и «ИЛИ» удобно использовать для вычисления булевых функций, заданных в виде ДНФ (дизъюнктивной нормальной формы).
В простейшем случае ПЛМ представляет матрицу – сеть горизонтальных и вертикальных шин. В узлах матрицы могут быть (а могут и не быть) полупроводниковые диоды.
Если в узле есть диод, то горизонтальная шина через него связана с вертикальной, если диода нет – то не связана. Каждая вертикальная шина такой матрицы – это простейший диодный элемент «И» или «ИЛИ» (в зависимости от направления включения диода и значения напряжения на резисторах матрицы).
На рис. 3.29 приведен пример двух матриц – «И» и «ИЛИ». Каждая вертикальная линия в этих матрицах – это один диодный логический элемент «И» или «ИЛИ». На входы матриц подаются напряжения UxI, соответствующие логическим переменным xI. Значению xI=0 в матрице соответствует UxI=0 [В], значению xI = 1 соответствует UxI=Uип [В], где Uип – напряжение источника питания в вольтах. Выходные напряжения матриц UуI соответствуют значениям функций уI , реализуемых данными матрицами. Причем нетрудно заметить, что в матрице «ИЛИ» UуI=Uип (уI =1), если в узле матрицы на пресечении линий UуI и UxJ есть диод и UxJ=Uип (xJ=1). В матрице «И» UуI=Uип (уI =1), если на всех входах, соединенных диодами с шиной UуI, значения UxJ=Uип (xJ=1) и UуI=0 В (уI =0), если хотя бы на одном из входов UxJ= 0 В (xJ=0).
Таким образом, в примере (см. рис. 3.29) матрица «ИЛИ» реализует три функции У1, У2, У3 от трех переменных x1, x2 , x3 :
У 1 = x1 Ú x3 ; У 2 = x1 Ú x2 ; У 3 = x2 Ú x3 ,
а матрица «И» реализует функции
У 1 = x1 x3 ; У 2 = x1 x2 ; У 3 = x2 x3 .
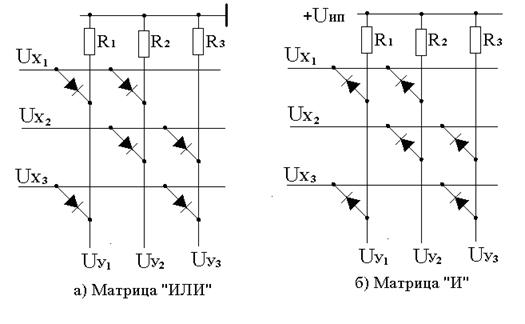
Рис. 3.29
На рис. 3.29 матрицы изображены фактически как принципиальные схемы, в которых логические переменные xI представлены напряжениями UxI , а функции уI – напряжениями UуI . В функциональных схемах будем использовать более простое изображение матриц: в узлах вместо диодов будем ставить точки, а входные и выходные сигналы будем обозначать как xJ и уI (рис. 3.30).
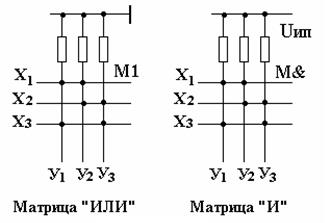
Рис. 3.30
Обычно матрицы используют тогда, когда необходимо реализовать семейство булевых функций от одних и тех же аргументов. Рассмотрим пример такой реализации.
Пусть дана система из трех булевых функций у1, у2, у3 от четырех переменных x1, x2, x3, x4:
y1 = Øx1 x2 Ú x1 Øx2Øx4 Ú x1 x3 x4;
y2 = Øx1 x2 Ú Øx1 Øx3 x4 Ú Øx1 Øx2 Øx3Ú Øx2 Øx4;
y3 = x1 Øx2 Øx4 Ú x1 Øx3 Ú Øx1 Øx2 Øx3.
Введем вспомогательные переменные ТI , через которые выразим все дизъюнктивные термы, встречающиеся в функциях у1, у2, у3 :
Т1= Øx 1 x 2 ; Т 2= x 1 Øx 2Øx 4 ; Т 3= x 1 x 3 x 4 ; Т 4= Øx 1 Øx 3 x 4;
Т 5 = Øx 1 Øx 2 Øx 3 ; Т 6= Øx 2 Øx 4; Т 7 = x 1 Øx 3 .
Выразим функции у1, у2, у3 через переменные ТI :
y1 = Т1 Ú Т 2 Ú Т 3;
y2 = Т1 Ú Т 4 Ú Т 5 Ú Т 6;
y3 = Т2 Ú Т 7 Ú Т 5.
В этих функциях через переменные ТI обозначены термы (логические произведения), которые вычисляются матрицей «И». С выходов матрицы «И» (М&), сигналы, соответствующие термам ТI, подаются на входы матрицы «ИЛИ» (М1), где вычисляются значения функций y1, y2 и y3 . Схема приведена на рис. 3.31.
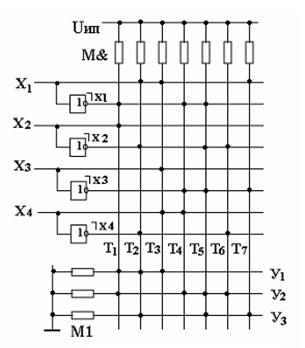
Рис. 3.31
С помощью матриц М& («И») и М1 («ИЛИ») можно реализовывать не только дизъюнктивные нормальные форм, но и скобочные выражения, которые часто являются более компактными.
Например, даны две функции:
y1 = (x1 x2 Ú Øx1 Øx2) x3 Ú Ø(x1 x2 Ú Øx1 Øx2) Øx3;
y2 = x1 x2 Ú Ø(x1 x2 Ú Øx1 Øx2) x3.
Заметим, что выражение в скобках – (x1 x2 Ú Øx1 Øx2) – три раза встречается в функциях y1 и y2.
На матрицах М& («И») и М1 («ИЛИ») сформируем функцию f = x1x2 Ú Øx1Øx2 , затем эту функцию используем в матрице М& («И») для формирования термов, а затем и значений функций y1 и y2. Введем переменные ТI :
Т1 = x1 x2 ; Т2 = Øx1 Øx2 .
Через Т1 и Т2 выразим функцию f :
f = Т1 Ú Т2 .
Введем еще три переменные ТI , в которых кроме x1, x2, x3 используем функцию f:
Т3 = f Ù x 3; Т4 = Øf Ù Øx 3; Т5 = Øf Ù x 3.
Преобразуем функции y1 и y2 и запишем их в следующем виде:
y1 = (Т1Ú Т2) x 3 Ú Ø( Т1Ú Т2) Øx 3 = f Ù x 3 Ú Øf Ù Øx 3 = Т3 Ú Т4;
y2 = Т1Ú Ø( Т1Ú Т2) x 3= Т 1 Ú Øf Ù x 3= Т1 Ú Т5.
Таким образом, порядок вычислений функций y1 и y2 следующий. Матрица М& вычисляет Т1 = x1 x2 и Т2 = Øx1 Øx2, затем матрица М1 вычисляет f = Т1 Ú Т2 . Значение f в прямом и инверсном виде подается на вход матрицы М& , где вычисляются Т3, Т4 и Т5 , а затем матрица М1 вычисляет y1 = Т3 Ú Т4 и y2 = Т1 Ú Т5 . На рис. 3.32 приведена схема, реализующая данный способ вычисления скобочных булевых функций.

Рис. 3.32
3.3.2. Простейшая матричная реализация автомата Мили
Рассмотрим реализацию автомата Мили на ПЛМ на примере из п. 3.1.2. Отличие в синтезе автомата Мили на ПЛМ состоит только на этапах построения обратной структурной таблицы и функциональной схемы автомата.
Возьмем за основу структурную таблицу автомата Мили на жесткой логике из п. 3.1.2. Будем использовать в качестве элементов памяти состояний D-триггеры. Добавим в таблицу еще один столбец Тamas, в который будем записывать функции переходов: Тamas = am Ù Xamas , где Xamas – конъюнкция логических условий, обеспечивающих данный переход из am в as; am – состояние автомата, из которого начинается переход, представленное кодом состояния Kam , заданного значениями Q1Q0 на выходах элементов памяти Т1 Т0. Если, например, код состояния am имеет значение Kam = 10, то значения на выходах элементов памяти состояний Q1Q0 также равны 10. Так как здесь Q1=1, то Q1 войдет в функцию перехода без инверсии, а Q0 = 0 поэтому войдет в функцию с инверсией. Например, для пятой строки структурной таблицы автомата функция перехода из a2 в a3 имеет вид Т2 =a2x1; так как Ka2 =01, то Т1 = ØQ1Q0x1.
Обратная структурная таблица автомата Мили с памятью состояний на D-триггерах (для матричной реализации) имеет вид (табл. 3.13).
Структурная схема автомата Мили на матрицах (простейшая реализация) имеет вид, показанный на рис. 3.33. В схеме автомата используются две матрицы – М& («И»), которая используется для вычисления функций переходов Тamas, и М1 («ИЛИ»), выполняющая две функции – вычисление функций (Famas) управления элементами памяти состояний ПС) D1 и D0 и вычисление функций выходов (Yamas) автомата yi.
Таблица 3.13
| № п/п | am | Kam | as | Kas | Xamas | Yamas | Fa ma s | Тamas |
| a 1 a 4 | a 1 | Ø x 3 x 2 | - y7 | - - | Т1 = ØQ1 ØQ0 Øx3 Т2 = Q1 Q0 x2 | |||
| a 1 a 4 | a 2 | x 3 Ø x 2 | y1, y2 y6 | D0 D0 | Т3 = ØQ1 ØQ0 x3 Т4 = Q1 Q0 Øx2 | |||
| a 2 | a 3 | x 1 | Y 3 | D1 | Т5 = ØQ1 Q0 x1 | |||
| a 2 a 3 | a 4 | Ø x 1 | y4, y5 y4, y5 | D1, D0 D1, D0 | Т6 = ØQ1 Q0 Øx1 Т7 = Q1 ØQ0 |
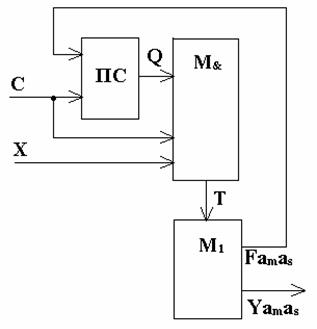
Рис. 3.33
Функции D1 , D0 и yi для нашего примера находятся как дизъюнкции соответствующих функций переходов Тamas:
D1 = T5 Ú T6 Ú T7 ; D0 = T3 Ú T4 Ú T6Ú T7 ;
y1 = y2 = T3 ; Y3 = T5 ; y4 = y5 = T6Ú T7 ; y6 = T4 ; y7 = T2 .
Как видно из этих выражений, функция переходов Т1 не используется ни в одной из функций Di и yi, поэтому ее можно не вычислять. Таким образом, функциональная схема автомата Мили на ПЛМ (для нашего примера) будет состоять из следующих элементов.
– Память состояний. В нашем примере – два D-триггера: Т1 Т0.
– Инверторы для формирования инверсных значений логических условий xI .
– Матрица М&, имеющая шесть вертикальных шин (по количеству формируемых функций переходов Тamas) и одиннадцать горизонтальных (удвоенное количество элементов памяти и логических условий плюс один – шина для сигнала синхронизации С).
– Матрица М1 , имеющая шесть вертикальных шин (по количеству используемых функций переходов Тamas) и семь горизонтальных (количество функций управления элементами памяти и функций переходов).
Функциональная схема автомата приведена на рис. 3.34.
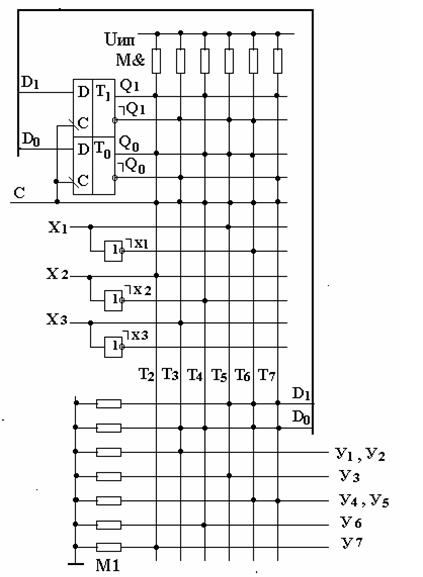
Рис. 3.34
Для упрощения схемы в ней не показаны элементы, используемые для установки автомата в начальное состояние и фиксации значений логических условий при поступлении импульса синхронизации С (смотри автомат Мили на жесткой логике).
Матрицы М& и М1 характеризуются площадями SM& и SM1, вычислить которые для каждого конкретного примера можно по структурной таблице автомата (или по функциональной схеме). Например, площадь SM& = 66: 11 горизонтальных шин и 6 вертикальных. Как видно из простого примера на рис. 3.34, площади матриц М& и М1 используются неэффективно по двум причинам:
1) при общем количестве логических условий ½X½= 3 в каждом конкретном переходе из am в as участвует всего одно;
2) при общем количестве ½Y½=7, на каждом переходе автомат вырабатывает всего одну микрокоманду.
Дата добавления: 2015-08-11; просмотров: 1225;
