Лекция 12.
Раздел 7. Синтез цифровых автоматов на жесткой логике
Тема 7.1. Структурный синтез МПА на жесткой логике. Синтез МПА автоматов Мура
На жесткой логике. Вопросы оптимизации МПА
Управляющие автоматы с жесткой логикой являются самыми быстродействующими, но схемные решения автоматов будут зависеть от их функций. Результатом синтеза автомата на жесткой логике является функциональная схема автомата, реализованная на логических элементах.
Элементная база автоматов на жесткой логике состоит из простейших логических элементов: конъюнкторов (элементы «И»), дизъюнкторов (элементы «ИЛИ»), инверторов (элементы «НЕ»), их комбинаций (элементы «И-НЕ», «ИЛИ-НЕ», «И-ИЛИ-НЕ» и т.п.), а также включает в себя и более сложные элементы – дешифраторы (DC), мультиплексоры (MS), элементы памяти (триггера).
Простейшие логические элементы реализуют вычисление простейших булевых функций. Примеры некоторых элементов, их обозначения и реализуемые ими функции приведены на рис. 3.5.
Символ «Ø» обозначает инверсию, «&» – конъюнкцию, «Ú» – дизъюнкцию. Часто вместо символа «&» используют «*», а в случае однобуквенных переменных – вообще его опускают, например функции, приведенные на рисунке, можно записать так: y = a b; y = Ø (a b Ú c d Ú e).
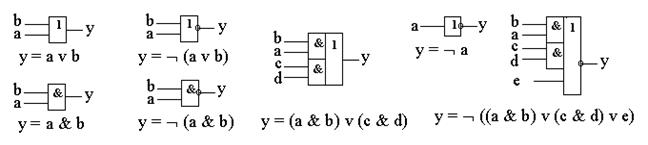
Рис. 3.5
Используя простейшие логические элементы можно строить функциональные схемы, реализующие сложные булевы функции, например построить функциональную схему, реализующую вычисление следующей системы булевых функций
y1 = x2 Ø x1 x0 Ú Ø x2 x1 x0 Ú Ø x2 Ø x1 Ø x0 ;
y2 = x2 Ø x1 x0 Ú Ø x2 x0 Ú x2 Ø x0 ;
y3 = x2 Ø x0 Ú Ø x2 x0 Ú Ø x1.
В приведенном примере в функциях y1 , y2 , y3 встречаются одинаковые конъюнкции, которые обозначим через вспомогательные переменные Z i и выразим через x i:
Z1 = x2 Ø x1 x0; Z2 = Ø x2 x1 x0; Z3 = Ø x2 Ø x1 Ø x0 ;
Z4 = Ø x2 x0; Z5 = x2 Ø x0.
Выразим функции y1 , y2 , y3 через дизъюнкцию Z i :
y1 = Z1Ú Z2 Ú Z3; y2 = Z1Ú Z4 Ú Z5; y3 = Z5Ú Z4 Ú Ø x1 .
Функциональные схемы строятся по следующим правилам.
1. Входы схемы (переменные x i) – с левой стороны схемы, выходы (переменные y i) – с правой стороны.
2. Входы схемы (переменные x i), значения которых используются в функциях с инверсиями, соединяются с входами инверторов, на выходах которых формируются значения Ø x i.
3. Схемы, вычисляющие значения Z i , строятся на конъюнкторах, на входы которых подаются соответствующие переменные x i или Ø x i.
4. Схемы, вычисляющие значения y i , строятся на дизъюнкторах, на входы которых подаются соответствующие переменные xi ,Ø xi или Z i .
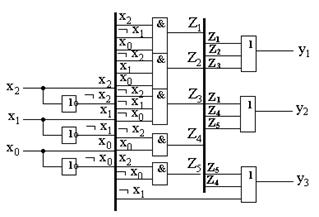
Рис. 3.6
5. Чтобы схема была легкочитаема, при ее изображении используют «шины». Шина изображается более толстой линией на схеме, в которую входят и из которой выходят тонкие линии, отображающие связи между элементами. Для идентификации этих связей непосредственно у шины ставятся либо обозначения соответствующих переменных, либо номера этих связей (первое предпочтительней). На рис. 3.6 приведена функциональная схема, реализующая функции y1, y2, y3 .
Дешифратор (DC) преобразует позиционный двоичный код (двоичное число) в унитарный. Унитарный код содержит «1» только в одном разряде. Входы дешифратора (в отличие от входов простейших логических элементов) характеризуются своим весом (как разряды двоичного числа): младший разряд имеет вес 1, следующий разряд – вес 2, n-разряд имеет вес 2 n-1. Веса разрядов указываются на входах дешифратора. Полный дешифратор имеет 2 n выходов, имеющих нумерацию от 0 до 2 n –1. Таким образом, дешифратор с двумя входами имеет 4 выхода, с тремя входами – 8 выходов и т.д. На рис. 3.7 приведено изображение дешифратора с двумя входами x1 x0 .
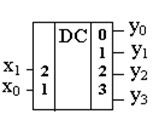
Рис. 3.7
Значения x1 x0 – двоичное число, указывающее номер выхода дешифратора, на котором будет сформирован сигнал «1». Функции yi, на выходе дешифратора имеют вид
y0 = Ø x1 Ø x0 ; y2 = x1 Ø x0 ;
y1 = Ø x1 x0 ; y3 = x1 x0 .
Функцию дешифратора можно пояснить также следующей таблицей истинности (табл. 3.3).
Таблица 3.3
| x1 | x0 | y0 | y1 | y2 | y3 |
Многие дешифраторы имеют еще один дополнительный вход – «разрешение работы дешифратора». На рис. 3.8 приведен пример такого дешифратора, который называется дешифратор – демультиплексор.
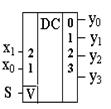
Рис. 3.8
Если на вход V подается «0», то на всех выходах дешифратора – нули; если на вход V подается «1», то дешифратор работает в соответствии с приведенной таблицей истинности, а функции yi, на выходе дешифратора имеют вид
y0 = S (Ø x1 Ø x0 ); y2 = S (x1 Ø x0 );
y1 = S (Ø x1 x0 ); y3 = S (x1 x0 ).
Мультиплексор (MS) выполняет функции электронного переключателя, позволяющего выбрать один из нескольких источников сигнала для одного приемника. Пример простейшего мультиплексора приведен на рис. 3.9.
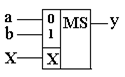
Рис. 3.9
У этого мультиплексора один управляющий вход (Х) и два информационных (a и b). Если на управляющий вход Х подать «0», то на выходе MS значение y = a, если на Х подать «1», то значение y = b. Другими словами, приведенный на рисунке MS – это переключатель на два положения, которым выбирается один из двух источников информации (a и b) для приемника У. Функцию MS можно описать выражением
y = Ø х a Ú х b.
Количество управляющих входов у MS может быть 2, 3 и более. В этом случае MS – это переключатель не на два, а на 2 n положений (где n – количество управляющих входов), позволяющий выбирать один из 2 n информационных входов. Номер этого информационного входа задается двоичным числом, подаваемым на управляющие входы: хn-1 ...х1 х0. На рис. 3.10 приведен пример MS с четырьмя информационными входами (a, b, c, d) и двумя управляющими (x1x0).

Рис. 3.10
Функцию MS такого можно описать выражением
y = a (Ø x1 Ø x0 ) Ú b (x1 Ø x0 ) Ú c (Ø x1 x0 ) Ú d (x1 x0 ).
Используя описанные выше функциональные элементы, можно строить так называемые комбинационные логические схемы (или цифровые автоматы комбинационного типа, автоматы без памяти), т.е. схемы, реализующие булевы функции. В микропрограммных автоматах, как правило, используются элементы памяти, на которых строится память состояний автомата.
Простейшим элементом памяти является статический асинхронный RS-триггер. RS-триггер – это элемент, имеющий два устойчивых состояния, которые обычно обозначают как «0» и «1» (рис. 3.11).
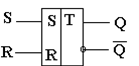
Рис. 3.11
Для установки RS-триггера в одно из устойчивых состояний «0» или «1» у него имеется два входа: R – для установки в состояние «0» и S – для установки в состояние «1». Выходы RS-триггера обычно обозначаются как Q (прямой выход) и ØQ (инверсный выход). Значение на выходе Q («0» или «1») обычно отождествляют с состоянием триггера «0» или «1». Если через Qt обозначить значение на выходе Q в момент времени t, а через Qt+1 – обозначить значение на выходе Q в момент времени t+1, то поведение RS-триггера можно описать следующей таблицей (табл. 3.4).
Из таблицы видно, что при R=0 и S=1 происходит установка триггера в состояние «1» (Qt+1 = 1), при R=1 и S=0 происходит установка триггера в состояние «0» (Qt+1 = 0). Эти установки происходят независимо от предыдущего состояния триггера Qt. При R=0 и S=0 триггер сохраняет свое состояние, а комбинация R=1 и S=1 является недопустимой, так как одновременно установить триггер в состояния «0» и «1» невозможно. На рис. 3.11 приведено изображение статического асинхронного RS-триггера.
Таблица 3.4
| R | S | Qt | Qt+1 | Комментарий |
| Хранение «0» | ||||
| Хранение «1» | ||||
| Установка в «1» | ||||
| Установка в «1» | ||||
| Установка в «0» | ||||
| Установка в «0» | ||||
| Х | Запрещенная комбинация R и S | |||
| Х | Запрещенная комбинация R и S |
Недостатком асинхронного RS-триггера является то, что изменение его состояния возможно в произвольный момент времени сразу же после изменения сигналов на его входах R и S, поэтому асинхронный RS-триггер часто используют как элемент памяти для построения синхронных триггеров. В синхронных триггерах изменение состояния возможно только в момент подачи на специальный вход «С» импульса синхронизации. Существуют триггеры, синхронизируемые импульсом С и фронтом импульса С. Фронтом импульса синхронизации называют переход значения С из «0» в «1» (положительный фронт) или из «1» в «0» (отрицательный фронт). Триггеры, синхронизируемые фронтом импульса С, нашли наибольшее применение в цифровых устройствах.
На рис. 3.12 приведено изображение двух RS-триггеров, синхронизируемых фронтом импульса синхронизации С. Наклонная черта на входе С показывает, по какому фронту импульса С – положительному (/) или отрицательному (\) – происходит переход триггера из одного состояния в другое.
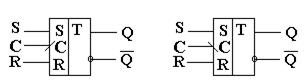
Рис. 3.12
Кроме RS-триггеров широкое применение в цифровых устройствах нашли D-триггеры и JK-триггеры (также синхронизируемые фронтом импульса С).
D-триггер, в отличие от RS-триггера, имеет всего один информационный вход – D. Синхронный D-триггер изменяет свое состояние также в момент поступления на его вход «С» импульса синхронизации С. Новое состояние Qt+1 не зависит от предыдущего Qt , а зависит только от значения на входе D в момент поступления импульса С на вход С триггера. JK-триггер называется универсальным, так как на его основе можно реализовать функции других триггеров. Закон его функционирования можно представить в виде табл. 3.5.
На рис. 3.13 приведены изображения D-триггера, синхронизируемого положительным фронтом импульса С, и JK-триггера, синхронизируемого отрицательным фронтом импульса С.
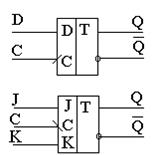
Рис. 3.13
Автоматы с жесткой логикой обычно строятся или как автоматы Мура, или как автоматы Мили. Поскольку функционирование и тех, и других зависит не только от входных сигналов (логических условий Xi), но и от текущего состояния автомата, необходимым элементом УА является память состояний. В качестве элементов памяти обычно используются триггеры различных типов: RS-, D-, JK-, T-триггеры, синхронизируемые фронтом (положительным или отрицательным) импульса синхронизации С. По фронту импульса С автомат переходит из одного состояния в другое. Выходные сигналы автомата – микрокоманды – также вырабатываются синхронно с импульсом С.
Таблица 3.5
| K | J | Qt | Qt+1 | Комментарий |
| Хранение «0» | ||||
| Хранение «1» | ||||
| Установка в «1» | ||||
| Установка в «1» | ||||
| Установка в «0» | ||||
| Установка в «0» | ||||
| Изменение состояния на противоположное | ||||
| Изменение состояния на противоположное |
Различие автоматов Мура и Мили следующее: в автомате Мура вырабатываемая автоматом микрокоманда Yi зависит только от текущего состояния автомата, а в автомате Мили – от текущего состояния и значений логических условий на входе автомата.
Синтез автомата Мура по ГСА. Простейшая реализация
Разметка состояний автомата Мура по ГСА
Каждой операторной вершине ГСА автомата Мура соответствует определенное состояние – ai . Начальное состояние автомата соответствует началу ГСА, а точнее – входу в первую вершину ГСА. Первая вершина ГСА обычно соответствует логическому условию «Пуск», поэтому начальное состояние можно отметить на входе этой вершины. Поскольку этому состоянию не соответствует никакая операторная вершина, то и автомат в начальном состоянии не выдает никаких микрокоманд.
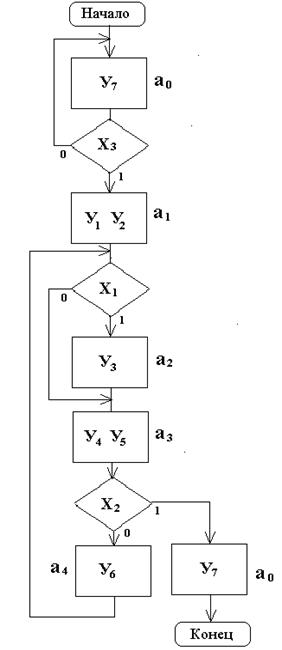
Рис. 3.14
При такой отметке начального состояния конечное состояние автомата соответствует завершению ГСА (перед вершиной «Конец»).
Для корректной работы автомата необходимо, чтобы после завершения выполнения алгоритма автомат вернулся в начальное состояние. Таким образом можно совместить начальное и конечное состояния автомата и обозначить их одинаково a0.
Часто дополнительно введенную операторную вершину, соответствующую микрокоманде «Операция выполнена», отмечают как конечное состояние автомата (a0), а так как конечное состояние автомата должно совпадать с начальным, в ГСА вводится еще одна дополнительная операторная вершина, которая отмечается состоянием a0, так же, как конечная (рис. 3.14). Такое преобразование ГСА имеет определенные преимущества: если автомат «свободен», он не «молчит», а выдает микрокоманду «Операция выполнена», что говорит о его готовности к работе.
Остальным операторным вершинам соответствуют состояния, которые можно пронумеровать так: a1, a2, a3 и т.д. (см. рис. 3.14).
Таким образом, ГСА автомата Мура (рис. 3.14 в нашем примере) отличается от исходной ГСА (см. рис. 3.2) еще одной дополнительной вершиной с состоянием a0. Обе вершины, помеченные состоянием a0, можно мысленно совместить, так как после завершения операции автомат должен вернуться в начальное состояние
3.1.1.2. Построение графа переходов автомата Мура
(по ГСА рис. 3.14)
Вершины графа соответствуют состояниям автомата, дуги – переходам из состояния am в состояние as. У вершин графа записываются микрокоманды, соответствующие состояниям, в начале дуги – логические условия, определяющие переход из состояния am в состояние as (рис. 3.15).
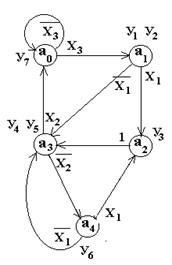
Рис. 3.15
3.1.1.3. Построение прямой таблицы переходов автомата Мура
Прямая таблица переходов (табл. 3.6) строится по графу переходов (см. рис. 3.15). Количество строк в таблице равно количеству переходов в графе. В столбце аm записываются состояния, из которых начинается переход, в столбце as – состояния, в которые перешел автомат из аm. В столбце Yas записываются Yi – микрокоманды, вырабатываемые автоматом в состоянии as. В столбце Xamas записываются логические условия (их конъюнкция), обеспечивающие переход из состояния аm в состояние as. Прямая таблица позволяет проверить полноту переходов, показанных на графе переходов: дизъюнкция всех Xa ma s из состояния a m должна быть равна «1». В нашем примере дизъюнкция всех Xa0 a s равна Ø x 3 Ú x 3 = 1 .
Таблица 3.6
| № п/п | am | a s | Yas | Xamas |
| a 0 | a 0 a 1 | y7 y1, y2 | Ø x 3 x 3 | |
| a 1 | a 2 a 3 | y3 y4, y5 | x 1 Ø x 1 | |
| a 2 | a 3 | y4, y5 | ||
| a 3 | a 4 a 0 | y6 y7 | Ø x 2 x 2 | |
| a 4 | a 2 a 3 | y3 y4, y5 | x 1 Ø x 1 |
3.1.1.4. Кодирование состояний автомата. Выбор элементов памяти
Так как поведение автомата всегда зависит от его текущего состояния аm, необходимо хранить код состояния аm в памяти состояний автомата. Объем памяти зависит от способа кодирования состояний. При минимальном кодировании каждому состоянию соответствует число в двоичном представлении, причем количество разрядов этого числа n определяется выражением n = ] log2 | A | [. Другой крайний случай – унитарное кодирование, при котором n = | A | . От выбранного способа кодирования и самого кодирования состояний может зависеть сложность схемы автомата.
Используем для нашего примера минимальное кодирование состояний. Так как автомат имеет пять состояний, то минимальное количество элементов памяти
n = ] log2 | A | [ = ] log2 5 [ = 3.
Выберем в качестве элементов памяти D-триггеры. Для нашего примера их количество равно трем. Обозначим их как Т2 , Т1 , Т0 , причем Т2 соответствует старшему разряду кода состояний. Выходы триггеров обозначаются соответственно Q2, Q1, Q0. Значение числа Q2Q1Q0 на этих выходах есть код состояния автомата.
Закодируем состояния автомата произвольно (Ka i = Q2Q1Q0):
К а0 = 100. К а1 = 001. К а2 = 010.
К а3 = 000. К а4 = 011.
3.1.1.5. Обратная структурная таблица автомата Мура
Обратная структурная таблица автомата Мура (табл. 3.7) строится на основе прямой таблицы переходов путем упорядочивания строк по столбцу as и добавления столбцов:
Ka m – код состояния a m;
Ka s – код состояния a s.
F a m a s – функции управления элементами памяти при переходе из состояния a m в состояние a s. Поскольку в качестве элементов памяти используем D-триггеры, в этом столбце записываем только Di, соответствующие триггерам, которые необходимо установить в состояние «1», чтобы обеспечить переход в состояние с кодом K a s.
Таблица 3.7
| № п/п | a m | Kam | a s | Kas | Xamas | Yas | Famas |
| a 0 a 3 | a 0 | Ø x 3 x 2 | y 7 | D 2 D 2 | |||
| a 0 | a 1 | x 3 | y 1, y 2 | D 0 | |||
| a 1 a 4 | a 2 | x 1 x 1 | y 3 | D 1 D 1 | |||
| a 1 a 2 a 4 | a 3 | Ø x 1 Ø x 1 | y 4, y 5 | - - - | |||
| a 3 | a 4 | Ø x 2 | y 6 | D 1 D 0 |
3.1.1.6. Функции управления элементами памяти
и функции выходов автомата
Функции управления элементами памяти записываются по обратной структурной таблице автомата:
D i = F( a m , X a m a s).
Смысл этого выражения следующий (например для D2): значение функции D2 должно быть равно 1 (см. обратную структурную таблицу) в двух случаях (1-я и 2-я строки таблицы): если автомат находился в состоянии a0, а значение x 3 = 0; если автомат находился в состоянии a3, а значение x 2 =1. Таким образом, функция D 2 имеет вид
D 2 = a0Øx 3 Ú a3 x 2.
Остальные функции D 1 и D 0 записываются аналогично:
D 1 = a1 x 1 Ú a4 x 1 Ú a3Øx 2 = x 1 (a1 Ú a4) Ú a3 Øx 2.
D 0 = a0 x 3 Ú a3Øx 2.
Функции выходов также записываются по обратной структурной таблице автомата:
y i = F( a s).
Так как yi в автомате Мура зависят только от текущего состояния автомата, то для нашего примера они имеют вид
y1 = y2 = a1. y3 = a2. y4 = y5 = a3. y6 = a4. y7 = a0.
Это означает следующее: в состоянии a1 автомат вырабатывает микрокоманды y1 и y2 , в состоянии a2 – микрокоманду y3 и т.д.
3.1.1.7. Структурная схема автомата Мура на жесткой логике
Структурная схема автомата Мура состоит из следующих цифровых узлов (рис. 3.16).
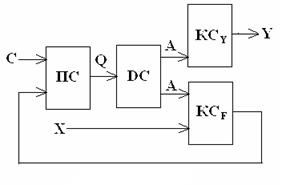
Рис. 3.16
Память состояний (ПС), дешифратор состояний (DC), комбинационная схема формирования сигналов управления элементами памяти состояний (КСF), комбинационная схема формирования выходных сигналов автомата (КСУ). Взаимодействие узлов автомата следующее. Автомат находится в некотором состоянии am, код которого Kam в виде значений Q на выходе триггеров памяти состояний (ПС) подается на вход дешифратора состояний (DC), на выходе которого собственно и формируются значения переменных am. На выходах комбинационной схемы КСУ формируются микрокоманды У, а на выходах схемы КСF формируются значения функций управления элементами памяти, которые обеспечивают переход автомата в новое состояние a s при поступлении импульса синхронизации С на вход синхронизации ПС.
3.1.1.8. Функциональная схема автомата Мура на жесткой логике
Функциональная схема автомата Мура состоит из следующих цифровых узлов.
· Память состояний. В нашем примере – триггеры Т2, Т1, Т0.
· Дешифратор состояний DC. Дешифратор необходим для преобразования двоичного кода состояний автомата Ka m в унитарный, соответствующий переменным a i , используемым в записанных выше функциях. В нашем примере дешифратор DC имеет 3 входа и 8 выходов. На вход DC подается Kam – код состояния am , а на выходах DC формируется унитарный код состояния автомата a m: единица на i-том выходе дешифратора DC формируется при Kam = i.
· Комбинационная схема формирования сигналов управления элементами памяти состояний автомата реализует функции
D i = F( a m , X a m a s)..
· Комбинационная схема формирования выходных сигналов автомата реализует функции y i = F( a s).
В функциональной схеме (рис. 3.17) использованы «шины». Шины представляют собой множество соединений схемы, изображенных в виде одной утолщенной линии. Вход в шину и выход из нее конкретного соединения обозначаются либо одним и тем же числом, либо содержательным обозначением сигнала, передаваемого по этому соединению. Применение шин в схемах позволяет избежать большого числа пересечений на схеме и делает ее более простой для чтения.
С целью упрощения схемы в ней не показаны элементы, обеспечивающие установку автомата в начальное состояние а0 с кодом Ка0 = 100. Этот вопрос будет рассмотрен ниже.
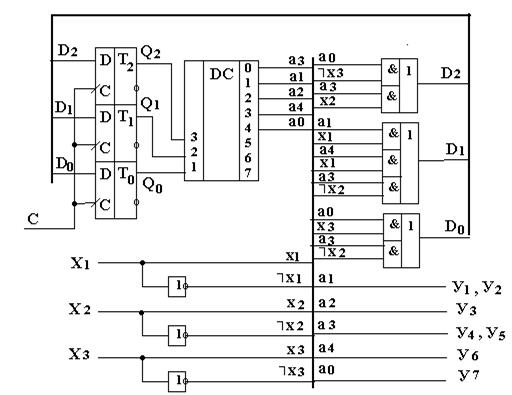
Рис. 3.17. Функциональная схема Мура
На рис. 3.18 приведены временные диаграммы, поясняющие работу автомата Мура. Находясь в некотором состоянии a i, автомат вырабатывает выходной сигнал (микрокоманду) yj, соответствующий этому состоянию. В это же время формируются сигналы управления элементами памяти D i, которые определяют следующее состояние автомата в зависимости от текущего и значений логических условий xi. При поступлении на вход синхронизации автомата положительного фронта импульса С автомат переходит в новое состояние, определяемое значениями Di на входах триггеров Т2 Т1 Т0.
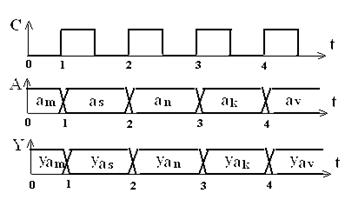
Рис. 3.18
Дата добавления: 2015-08-11; просмотров: 1696;
