Лекция 13. Тема 7.2. Структурный синтез МПА на жесткой логике
Тема 7.2. Структурный синтез МПА на жесткой логике. Синтез МПА автоматов
Мили на жесткой логике. Вопросы оптимизации МПА
Разметка состояний автомата Мили по ГСА
В отличие от автомата Мура состояния автомата Мили не соответствуют операторным вершинам ГСА, а отмечаются на дугах ГСА перед вершинами, следующими за операторными. Исключение составляет начальное (оно же конечное) состояние автомата. Его удобно обозначать символом а0 или а1. Символом а0 или а1 отмечают вход вершины, следующей за начальной, и вход конечной вершины ГСА. Входы всех остальных вершин, следующих за операторными, также отмечаются символами: а1, а2, … Используем для примера ГСА УА (см. рис. 3.2) для синтеза автомата Мили. Обозначим начальное состояние как а1, а остальные – а2, а3, а4.
В случае, когда в вершину, следующую за операторной, входит более чем одна дуга, состояние необходимо отметить на дуге так, чтобы для всех входящих дуг соблюдалось правило разметки состояний. На ГСА (рис. 3.19) это состояния а2 и а3. Состояние а2 необходимо отметить ниже входящей слева стрелки, а состояние а3 – выше входящей справа стрелки. В первом случае в а2 сошлись пути из двух операторных вершин, а во втором – путь из а2 не приводит в состояние а3 (этот переход был бы «пустым», без прохода через операторную вершину), а приводит в состояние а4 (после операторной вершины).
3.1.2.2. Построение графа переходов автомата Мили по ГСА
Вершины графа соответствуют состояниям автомата, дуги – переходам из состояния am в состояние as. У выхода дуги из вершины графа am записываются логические условия, определяющие переход из состояния am в состояние as , а у входа дуги в состояние as – микрокоманды, вырабатываемые автоматом при переходе из состояния am в состояние as (рис. 3.20).
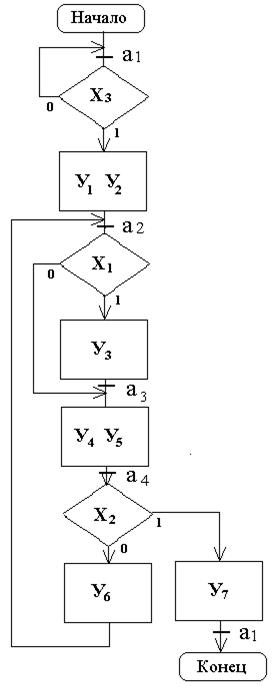
Рис. 3.19
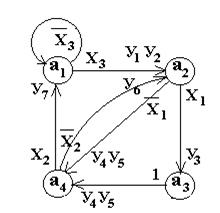
Рис. 3.20
3.1.2.3. Построение прямой таблицы переходов автомата Мили
Прямая таблица переходов (табл. 3.8) строится по графу переходов (см. рис. 3.20).
Количество строк в таблице равно количеству переходов в графе переходов. В столбце аm записываются состояния, из которых начинается переход, в столбце as – состояния, в которые перешел автомат из состояния аm.
Таблица 3.8
| № п/п | am | as | Xamas | Yamas |
| a 1 | a 1 a 2 | Ø x 3 x 3 | - y 1 y 2 | |
| a 2 | a 3 a 4 | x 1 Ø x 1 | y 3 y 4 y 5 | |
| a 3 | a 4 | y 4 y 5 | ||
| a 4 | a 1 a 2 | x 2 Ø x 2 | y 7 y 6 |
В столбце Y amas записываются Yi – микрокоманды, вырабатываемые автоматом при переходе из состояния am в состояние as. В столбце Xamas записываются логические условия (их конъюнкция), обеспечивающие переход из состояния аm в состояние as.
Прямая таблица позволяет проверить полноту переходов, показанных на графе переходов: дизъюнкция всех Xamas из состояния am должна быть равна «1» (ÈXamas=1). В нашем примере дизъюнкция всех Xa1as равна ÈXa1as = Xa1a1 Ú Xa1a2 = Ø x 3 Ú x 3 = 1. Аналогично ÈXa2as = Xa2a3 Ú Xa2a4 = x 1 Ú Øx 1 = 1, ÈXa3as = Xa3a4 = 1,
ÈXa4as = Xa4a1 Ú Xa4a2 = x2 Ú Øx2 = 1.
3.1.2.4. Кодирование состояний автомата. Выбор элементов памяти
Кодирование состояний автомата Мили производится так же, как и автомата Мура.
Используем для нашего примера минимальное кодирование состояний. Так как автомат имеет четыре состояния, то минимальное количество элементов памяти
n = ] log2 | A | [ = ] log2 4 [ = 2.
Выберем в качестве элементов памяти синхронные RS-триггеры. Для нашего примера их количество равно двум. Обозначим их как Т1, Т0 , причем Т1 соответствует старшему разряду кода состояний. Выходы триггеров обозначаются соответственно Q1, Q0. Значение числа Q1Q0 на этих выходах есть код состояния автомата. Закодируем состояния автомата произвольно (Ka i = Q1Q0):
К а1 = 00, К а2 = 01, К а3 = 10, К а4 = 11.
3.1.2.5. Обратная структурная таблица автомата Мили
Обратная структурная таблица (табл. 3.9) автомата Мили строится так же, как и для автомата Мура.
Таблица 3.9
| № п/п | a m | Kam | a s | Ka s | X a ma s | Y a m a s | F a m a s |
| a 1 a 4 | a 1 | Ø x 3 x 2 | - y 7 | - R 1 R 0 | |||
| a 1 a 4 | a 2 | x 3 Ø x 2 | y 1 y 2 y 6 | S 0 R 1 | |||
| a 2 | a 3 | x 1 | y 3 | S 1 R 0 | |||
| a 2 a 3 | a 4 | Ø x 1 | y 4 y 5 y 4 y 5 | S 1 S 0 |
При заполнении столбца F am as следует обратить внимание на то, что управление RS-триггерами отличается от управления D-триггерами. Если состояние некоторых разрядов RS-триггеров памяти автомата не изменяется при переходе из am в as , то нет необходимости вырабатывать соответствующие сигналы управления S=1 или R=1, так как комбинация S=0 и R=0 соответствует режиму хранения в RS-триггерах. Например, в третьей строке структурной таблицы описан переход из состояния a1 с кодом Kam = 00 (Q1 =0, Q0 =0) в состояние a2 с кодом Kas = 01 (Q1 =0, Q0=1). Чтобы обеспечить переход из a1 в a2, нужно сохранить значение Q1 =0, а в младший разряд памяти состояний Q0 – установить «1», поэтому в столбце Famas третьей строки записано «S 0», что означает S0=1. При поступлении на вход синхронизации памяти состояний синхроимпульса С триггер Т1 не изменит своего состояния (так как R1 =0 и S1 =0), а триггер Т0 перейдет из состояния «0» в состояние «1» (так как R0=0, а S0=1). В столбце Famas не будем записывать Ri = 0 или Si = 0, а будем записывать только те Ri и Si, значения которых должны быть равны «1».
3.1.2.6. Функции управления элементами памяти
и функции выходов автомата
Функции управления элементами памяти записываются по обратной структурной таблице автомата:
R i = F( a m , X a m a s);
S i = F( a m , X a m a s).
Смысл этих выражений следующий (например для R1). Значение функции R1 должно быть равно «1» (см. обратную структурную таблицу) в двух случаях (2-я и 4-я строки таблицы): если автомат находился в состоянии a4, а значение x2 = 1, или, если автомат находился в состоянии a4, а значение Øx2 =1. Таким образом, функция R1 имеет вид
R 1 = a 4 x 2 Ú a4Øx 2 = a4 .
Остальные функции Ri и Si записываются аналогично:
S 1 = a2 x 1 Ú a2 Øx 1 = a2 ;
R 0 = a 4 x 2 Ú a2 x 1 ;
S 0 = a 1 x 3 Ú a3.
Функции выходов автомата Yamas также записываются по обратной структурной таблице автомата:
y i = F( am , X am as).
Смысл этого выражения следующий (например для y4). Значение функции y4 должно быть равно «1» (см. обратную структурную таблицу) при переходе автомата из состояний a2 или a3 в состояние a4 (6-я и 7-я строки таблицы). Иначе: если автомат находился в состоянии a2, а значение Øx2 = 1, или, если автомат находился в состоянии a3, то при переходе автомата из состояний a2 или a3 в состояние a4 значение y4 должно быть равно «1». Таким образом, функция y4 имеет вид
y 4 = y 5 = a2 Øx 1 Ú a 3 .
Остальные функции выходов имеют вид
y 1 = y 2 = a 1 x 3 ; y 3 = a2 x1;
y 6 = a4Øx 2; y 7 = a4 x 2.
3.1.2.7. Структурная схема автомата Мили на жесткой логике
Структурная схема автомата Мили состоит из следующих цифровых узлов (рис. 3.21): память состояний (ПС), дешифратор состояний (DC), комбинационная схема формирования сигналов управления элементами памяти состояний (КСF), комбинационная схема формирования выходных сигналов автомата (КСУ). Взаимодействие узлов автомата следующее. Автомат находится в некотором состоянии am, код которого Kam в виде значений Q на выходе триггеров памяти состояний (ПС) подается на вход дешифратора состояний (DC), на выходе которого собственно и формируются значения переменных am. На выходах комбинационной схемы КСF формируются значения функций управления элементами памяти Famas, которые обеспечивают переход автомата в новое состояние as при поступлении импульса синхронизации С на вход синхронизации ПС, а на выходах комбинационной схемы КСУ при этом формируются значения функций выходов автомата Yamas.

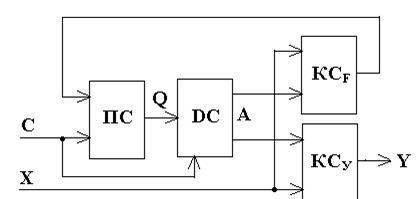
Рис. 3.21
3.1.2.8. Функциональная схема автомата Мили на жесткой логике
Функциональная схема автомата Мили состоит из следующих цифровых узлов.
· Память состояний. В нашем примере – два триггера Т1 Т0.
· Дешифратор состояний DC. В нашем примере – дешифратор DC имеет 2 входа и 4 выхода. На вход DC подается Kam – код состояния am , а на выходах DC формируется унитарный код состояния автомата a m: единица на i-том выходе дешифратора DC формируется при Kam = i.
· Комбинационная схема формирования сигналов управления элементами памяти состояний автомата. В нашем примере реализует функции
R i = F( am , X am as);
S i = F( am , X am as).
· Комбинационная схема формирования выходных сигналов автомата. В нашем примере реализует функции y i = F( a m , X a m a s).
· Память логических условий. В нашем примере это три D-триггера Тx1 Тx2 Тx3 . Значения логических условий на входе автомата Мили могут измениться во время формирования микрокоманды y i, что может привести к формированию «ложных» (лишних) микрокоманд, поэтому необходимо зафиксировать значения xi , поступившие на входы автомата к моменту прихода импульса синхронизации, на время формирования микрокоманд yi. Таким образом, по положительному фронту импульса синхронизации С значения x i, запоминаются на триггерах Тxi, при С = 1 формируются микрокоманды yi и функции управления элементами памяти R i и S i , а по отрицательному фронту импульса С автомат переходит в следующее состояние, определяемое значениями R i и S i на входах памяти состояний автомата.
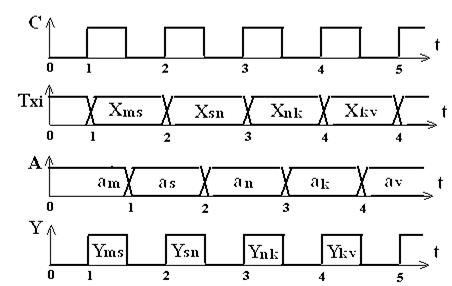
Рис. 3.22
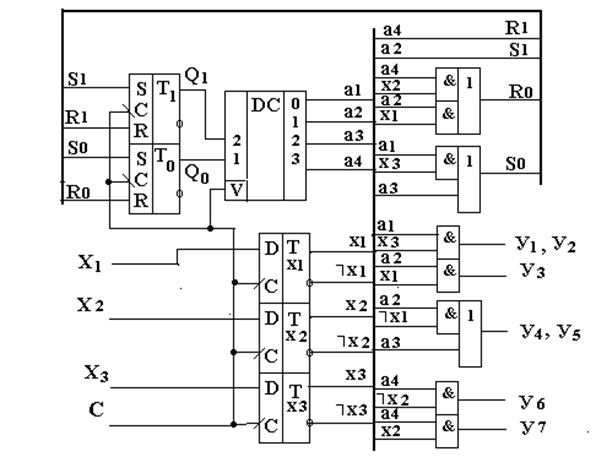
Рис. 3.23. Функциональная схема автомата Мили
Временная диаграмма, поясняющая работу автомата Мили, приведена на рис. 3. 22, функциональная схема – на рис. 3.23.
Из временной диаграммы видно, что по положительному фронту импульса синхронизации С значения логических условий Х на входе автомата запоминаются на триггерах Тxi. Значения логических условий с выходов этих триггеров и текущее состояние автомата a m используются для вычисления Уm s – микрокоманд, вырабатываемых автоматом на переходе из состояния a m в состояние a s . Дешифратор состояний DC (см. рис. 3.12) имеет вход разрешения V: при V=1 дешифратор выдает на одном из своих выходов значение «1», при V=0 – на всех выходах DC логический «0». Это означает, что при С=0 (а значит и V=0) все выходные сигналы автомата Уm s равны нулю. Автомат вырабатывает микрокоманды только при С=1.
Дата добавления: 2015-08-11; просмотров: 1170;
