Термодинамические процессы идеальных газов.

К основным процессам, имеющим большое значение, как для теоретических исследований, так и для практических работ в технике, относятся: изохорный, протекающий при постоянном объеме; изобарный, протекающий при постоянном давлении; изотермический,, протекающий при постоянной температуре; адиабатный, протекающий при отсутствии теплообмена с внешней средой.

Кроме того, существует группа процессов, являющихся при опре­деленных условиях обобщающими для основных процессов. Эти про­цессы называются политропными и характеризуются постоянством теплоемкости в процесса.

Для всех процессов устанавливается общий метод исследований, который заключается в следующем;

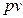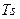выводится уравнение кривой процесса на - и -диаграммах;

устанавливается зависимость между основными параметрами ра­бочего тела в начале и конце процесса;

определяется изменение внутренней энергии по формуле, справед­ливой для всех процессов идеального газа:

,

или при постоянной теплоемкости:

;

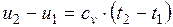вычисляется работа изменения объема газа по основной формуле:

;

определяется удельное количество теплоты, участвующее в процессе, по формуле:

;

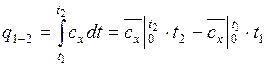определяется изменение удельной энтальпии в процессе по формуле, справедливой для всех процессов идеального газа:

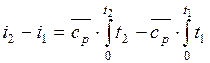
или для постоянной теплоемкости:

;

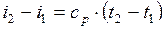определяется изменение удельной энтропии идеального газа по формулам:
,

.

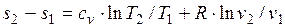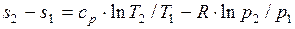Рассматриваемые процессы считаются обратимыми.

Изохорный процесс

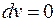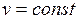Процесс, протекающий при постоянном объеме, называют изохорным ( , или ). Кривая процесса называется изохорой.

При постоянном объеме давление газа изменяется прямо пропорционально абсолютным температурам:

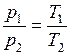. (1.17.1)

Внешняя работа газа при 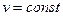равна нулю, так как 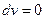. Следовательно,

.

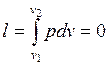Удельная располагаемая (полезная) внешняя работа 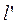, которая может быть передана внешнему объекту работы, равна:

.

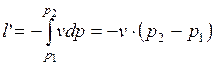Если процесс 1-2 осуществляется с увеличением давления, то удельное количество теплоты в нем подводится, при этом увеличиваются внутренняя энергия и температура газа. Если давление в процессе понижается, то удельное количество теплоты отводится, уменьшаются внутренняя энергия и температура газа.

Изменение удельной энтропии в обратимом изохорном процессе определяем из уравнения:

,

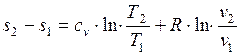Изменение энтропии при постоянной теплоемкости равно

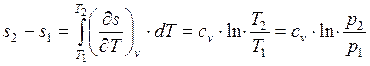. (1.17.2)

Как видно из данного уравнения, изохора на 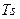– диаграмме пред­ставляет собой кривую 1-2 (рис. 1.17.1). Подкасательная к кривой 1–2 в любой ее точке дает значение истинной теплоемкости .

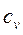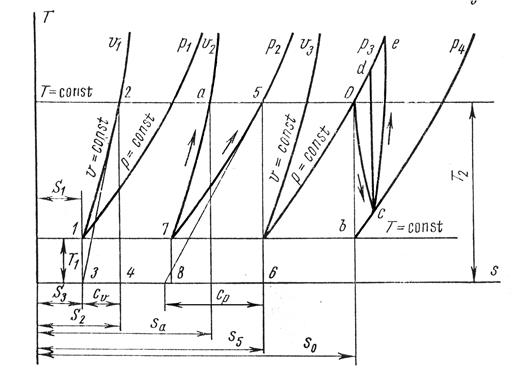
Рис. 1.17.1

Изобарный процесс

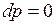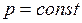Процесс, протекающий при постоянном давлении, называют изобарным ( , или ). Кривая процесса называется изобарой.

Это соотношение называется законом Гей-Люссака. Для процесса 1-2

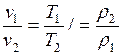. (1.17.3)

В изобарном процессе объемы одного и того же количества газа изменяются прямо пропорционально абсолютным температурам.

При расширении газа его температура возрастает, при сжатии – уменьшается.

Удельная работа изменения объема при этом выражается следую­щим уравнением:

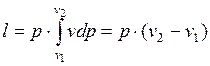, (1.17.4)

или

. (1.17.5)

Для обратимого изобарного процесса при постоянной теплоемкости изменение удельной энтропии находится по уравнению:

,

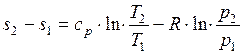Но при 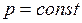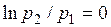, поэтому

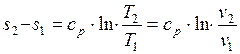. (1.17.6)

В случае изохорного и изобарного процессов в одном интервале тем­ператур возрастание энтропии будет больше в изобарном процессе, так как 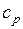всегда больше .

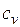Изотермный процесс

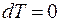Процесс, протекающий при постоянной температуре, называют изотермическим ( , или ). Кривая процесса называется изо­термой (рис. 18.2).

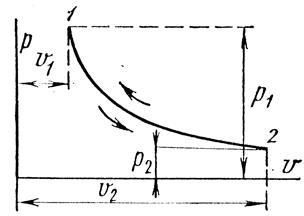
Рис. 1.17.2

и 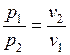(1.17.7)

При постоянной температуре объем газа изменяется обратно пропорционально его давлению (закон Бойля – Мариотта).

На 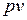– диаграмме изотермный процесс представляет собой равнобокую гиперболу.

Зная уравнение изотермного процесса для идеального газа, можно подсчитать работу процесса.

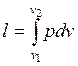
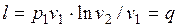. (1.17.8)

Удельная располагаемая внешняя работа 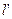определяется по фор­муле:

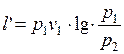, (1.17.9)

т. е. в изотермном процессе идеального газа 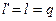, или удельная работа изменения объема, располагаемая (полезная) работа и удельное количество теплоты, полученное телом, равны между собой.

откуда

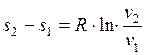и 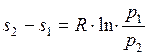(1.17.10)

Удельное количество теплоты, участвующее в изотермическом процессе, равно произведению изменения удельной энтропии 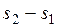на абсолютную температуру :

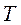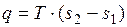
Адиабатный процесс

Процесс, протекающий без подвода и отвода теплоты, т. е. при от­сутствии теплообмена рабочего тела с окружающей средой, называют адиабатным.

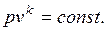(1.17.11)

При адиабатном процессе произведение давления на объем газа в степени 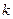есть величина постоянная. Величину 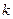называют показа­телем адиабаты. Рассмотрим зависимость между основными парамет­рами в адиабатном процессе.

Из уравнения адиабаты следует, что

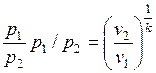и

.

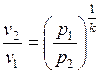
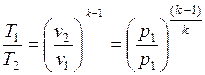Удельная работа изменения объема 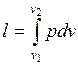, совершаемая телом над окружающей средой при равновесном адиабатном процессе, может быть вычислена по уравнению адиабаты

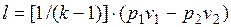. (1.17.12)

Из выражения (18.12) могут быть получены следующие формулы:

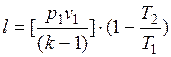и .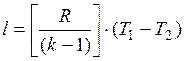

Вычислим располагаемую (полезную) внешнюю работу в адиабатном процессе, равную:

.

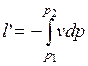Следовательно,

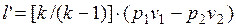(1.17.13)

И .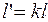

Политропные процессы

Условились всякий процесс идеального газа, в котором теплоем­кость является постоянной величиной, называть политропным про­цессом, а линию процесса – политропой.

Они протекают при постоянной теплоемкости.

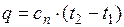(1.17.14)

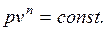(1.17.15)

Показатель политропы 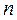принимает для каждого процесса опре­деленное числовое значение. Для основных процессов: изохорных 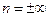, изобарных 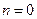, изотермических 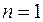и адиабатных .

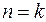Поскольку уравнение политропы отличается от уравнения адиа­баты только величиной показателя 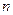, то, очевидно, все соотношения между основными параметрами могут быть представлены формулами, аналогичными адиабатному процессу:

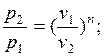
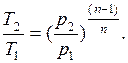
Уравнение удельной работы изменения объема, совершаемой телом при политропном процессе, имеет аналогичный вид с уравнением работы в адиабатном процессе, т. е.

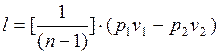(1.17.16)

Для конечного изменения состояния

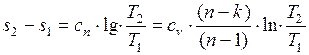. (1.17.17)