Теплоемкость газов. Энтропия.

Отношение элементарного количества теплоты 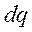, полученное телом при бесконечно малом изменении его состояния, к изменению температуры 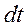называется удельной теплоемкостью тела в данном процессе:

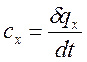(1.13.1)

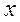Величина в уравнении зависит не только от интервала температур, но и от вита процесса подвода теплоты, характеризуемого некоторым постоянным параметром , которым может быть объем тела , давление 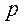и др. общее количество теплоты, полученное в данном процессе, определяется выражением

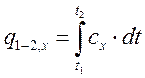(1.13.2)

На примере идеального газа. Имеем 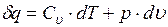, или заменив 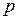на 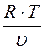, получим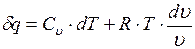

Разделив обе части последнего уравнения на 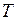, находим

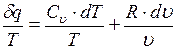(1.13.3)

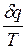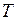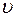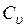Выражение при обратимом изменении состояния газа есть полный дифференциал некоторой функции переменных и ( зависит только от температуры, а - величина постоянная). Клаузиус назвал эту функцию энтропия и обозначил 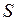в джоулях на градус (Дж/К).

Таким образом, дифференциал энтропии для обратимого изменения состояния определяется как

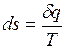(1.13.4)

Удельная энтропия является параметром состояния, и изменение ее в любом термодинамическом процессе полностью определяется крайними состояниями тела и не зависит от пути процесса.

Интегрируя определяем

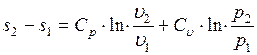(1.13.5)