Реальные газы. Водяной пар.

Реальные газы отличаются от идеальных газов тем, что молекулы этих газов имеют конечные собственные объемы и связаны между собой силами взаимодействия, имеющими электромагнитную и квантовую природу. Эти силы существуют между любыми молекулами при любых условиях и уменьшаются с увеличением расстояния между молекулами. При сближении молекул на малые расстояния силы притяжения резко уменьшаются и переходят в силы отталкивания, достигающие очень больших значений.

Из-за наличия сил взаимодействия между молекулами и ко­нечности их объема законы идеальных газов ни при каких условиях не могут быть строго применимы к реальным газам.

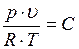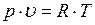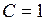При практических расчетах различных свойств реальных газов находит широкое применение отношение , которое по лучило название коэффициента сжимаемости. Так как для идеальных газов при любых условиях и , то коэффициент сжимаемости выражает отклонение свойств реального газа от свойств идеального. Значение 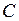для реальных газов в зависимости от давления и температуры может быть больше и меньше единицы, и только при очень малых давлениях и высоких температурах оно практически равно единице.

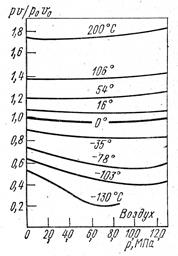
Рис. 1.23.1 Рис. 1.23.2

На рис. 1.24.1 показана зависимость 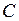от давления при темпе­ратуре 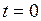°С для некоторых газов. Повышение давления и понижение температуры, увеличение концентрации молекул газа и уменьшение расстояния между ними усиливает отклонения свойств реального от свойств идеального газа. Из уравнения Клапейрона – Менделеева следует, что при любой постоянной температуре зависимость 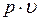от 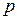должна изображаться прямой, параллельной оси давления. В действительности изотермы всех газов представляют собой кривыё даже в области не очень высоких давлений, а при давлениях от 20 МПа и выше кривые довольно круто поднимаются вверх.

Из рис. 1.23.2 для воздуха видно, что в области малых давлений, когда 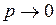, отношение 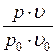стремится к конечному пределу: 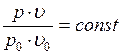. Из этого следует, что при малых 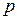и больших 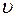произведение 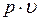изменяется очень мало и остается почти постоянным. Следовательно, чем больше разрежение, тем с большей точностью удовлетворяется уравнение Клапейрона – Менделеева для любого реального газа.

Температура, соответствующая изотерме с точкой минимума на оси ординат 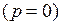, называется температурой Бойля. Изотерма, начинающаяся в точке Бойля, на некотором протяжении будет прямой, параллельной оси абсцисс, т. е. здесь точно соблюдается закон 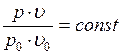. Все изотермы, начинающиеся выше температуры Бойля, имеют вид восходящих кривых. Для воздуха температура Бойля равна 54 °С.

Таким образом, свойства реальных газов как в количествен­ном, так и качественном отношениях значительно отличаются от свойств идеальных газов. Поэтому все результаты, полученные для реальных газов на основе законов идеальных газов, нужно рассматривать как приближенные и справедливые при очень больших разрежениях .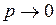

Отличие свойств любого реального газа от свойств идеального заставило ученых разрабатывать новые уравнения состояния, которые связывали бы значения 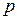, 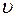и 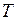и давали бы возможность рассчитывать некоторые свойства газов для разных условий, не прибегая к дорогостоящим, не всегда доступным прямым изме­рениям.

За последние 100 лет было предложено значительное число различных уравнений состояния реальных газов, но ни одно из них не решает проблему для общего случая.

Развитие кинетической теории газов позволило установить точное уравнение состояния реальных газов в таком виде:

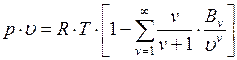
В этом уравнении коэффициенты 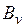при степенях в правой части уравнения, называемые вириальными коэффициентами, вы­ражаются через потенциальную энергию взаимодействия молекул данного газа и температуру 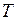, a 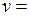2, 3, 4, ... – порядковый номер вириального коэффициента.

Однако полученное уравнение в общем виде не может быть использовано для непосредственных расчетов реальных газов.

В отдельных частных случаях, когда известен закон изменения потенциальной энергии взаимодействия между двумя молекулами в зависимости от расстояния между ними (так называемая потенциальная кривая) и при наличии определенного количества экспериментальных данных, может быть получено расчетное уравнение того или иного реального газа в довольно широком диапазоне изменения параметров. Из-за сложности вычисления вириальных коэффициентов обычно ограничиваются расчетом первых двух из них. Тогда расчетное уравнение имеет такой вид:

,

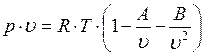где 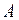и 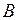– первый и второй вириальные коэффициенты, являю­щиеся функцией только температуры.

В настоящее время уравнения подобного вида получили широкое распространение при расчете свойств многих реальных газов.

Наиболее простым и качественно верно отражающим поведе­ние реального газа является уравнение Ван-дер-Ваальса, которое получается как частный случай из общего уравнения состояния Майера – Боголюбова, если пренебречь в правой части всеми членами, содержащими во второй степени и выше.

1.24. 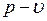и 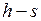диаграммы водяного пара.

Фазовая 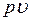– диаграмма системы, состоящей из жидкости и пара, представляет собой график зависимости удельных объемов воды и пара от давления.

Пусть вода при температуре 0 °С и некотором давлении 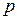за­нимает удельный объем 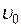(отрезок NS) (рис. 1.24.1). Вся кривая АЕ выражает зависимость удельного объема воды от давления при температуре 0 °С. Так как вода – вещество почти несжимаемое, то кривая АЕ почти параллельна оси ординат. Если при постоянном давлении сообщать воде теплоту, то ее температура будет повышаться и удельный объем увеличиваться. При некоторой температуре 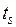вода закипает, а ее удельный объем 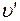в точке А' достигнет при данном давлении максимального значения. С увеличением давления растет температура кипящей жидкости 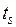и объем 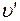также увеличивается.

График зависимости 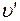от давления представлен на рис. 1.24.1 кривой АК, которая называется пограничной кривой жидкости. Характеристикой кривой АК является степень сухости .

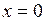Рис. 1.24.1

В случае дальнейшего подвода теплоты при постоянном давлении начнется процесс парообразования. При этом количества воды уменьшается, количество пара увеличивается.

В момент окончания парообразования в точке 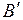пар будет сухим насыщенным. Удельный объем сухого насыщенного пара обозначается .

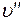Если процесс парообразования протекает при постоянном давлении, то температура его не изменяется и процесс А' В' является одновременно, изобарным и изотермическим. В точках А' и В' вещество находится в однофазном состоянии. В промежуточных точках вещество состоит из смеси воды и пара. Такую смесь тел называют двухфазной системой.

График зависимости удельного объема 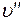от давления пред­ставлен на рис. 1.24.1 кривой KB, которая называется пограничной кривой пара. Характеристикой кривой KB является степень сухо­сти .

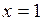Точка А соответствует состоянию кипящей жидкости в тройной точке ( 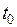=0,01 ° ≈ 0 °С), а изобара АВ соответствует состояниям равновесия всех трех фаз (тройная точка на 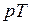–диаграмме). Эта изобара при выбранном масштабе изображения кривых практически совпадает с осью абсцисс.

Если к сухому насыщенному пару подводить теплоту при по­стоянном давлении, то температура и объем его будут увеличиваться и пар из сухого насыщенного перейдет в перегретый (точка D).

Обе кривые АК и KB делят диаграмму на три части. Влево от пограничной кривой жидкости АК до нулевой изотермы располагается область жидкости. Между кривыми АК и KB располагается двухфазная система, состоящая из смеси воды и сухого пара. Вправо от KB и вверх от точки К располагается область перегретого пара или газообразного состояния тела. Обе кривые АК и KB сходятся в одной точке К, которая называется критической точкой.

Критическая точка является конечной точкой фазового перехода жидкость — пар, начинающегося в тройной точке.

Выше критической точки существование вещества в двухфаз­ном состоянии невозможно. Никаким давлением нельзя перевести газ в жидкое состояние при температурах выше критической.

Параметры критической точки для воды: 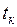=374,12 °С; 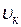= 0,003147 м3/кг; 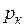=22,115 МПа; 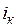= 2095,2 кДж/кг; 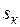= 4,424 кДж/(кг∙К).

Область, заключенная между изотермой воды при температуре 0 °С (линия АЕ) и осью ординат, представляет собой область равновесного сосуществования жидкой и твердой фаз.