Задачи к главе III для самостоятельного решения
1. На плоскости фиксированы две различные точки А и В; фиксировано положительное число k. Найти геометрическое место точек М, для каждой из которых 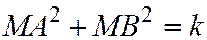 .
.
Отв. Пустое множество, если k< 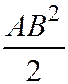 ; середина отрезка АВ, если k =
; середина отрезка АВ, если k = 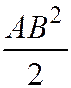 ; окружность с центром в середине отрезка АВ, если k >
; окружность с центром в середине отрезка АВ, если k > 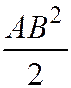 .
.
2. На плоскости фиксированы две различные точки А и В; фиксировано число k. Найти геометрическое место точек М, для каждой из которых 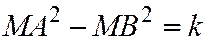 Отв. Прямая, перпендикулярная АВ.
Отв. Прямая, перпендикулярная АВ.
3. Дана точка О и прямая l, не проходящая через О. Пусть Р - переменная точка прямой l. На луче ОР берется точка М, такая, что 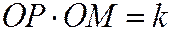 , где k-данное положительное число. Найти геометрическое место точек М.
, где k-данное положительное число. Найти геометрическое место точек М.
Отв. Окружность.
4. Написать в полярных координатах уравнение прямой, перпендикулярной полярной оси и отсекающей на ней отрезок ОA=а.
Отв.  .
.
5. Написать уравнение окружности радиуса а в полярных координатах, принимая за полюс точку О на окружности, а за полярную ось проходящий через нее диаметр ОА.
Отв. 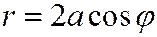 .
.
6. Прямоугольник, две стороны которого совпадают с осями координат, изменяется так, что его диагональ сохраняет постоянную величину а. Линия, описываемая основанием перпендикуляра, опущенного из вершины прямоугольника, противоположной началу координат, на его диагональ, называется астроидой. Найти ее уравнение, принимая за оси координат неподвижные стороны прямоугольника (рис. 70). Отв. 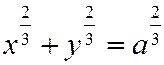 .
.
7. Даны точка О и прямая, находящаяся от точки О на расстоянии OA= а. Вокруг точки О вращается луч, пересекающий данную прямую в переменной точке B. На этом луче по обе стороны от точки В откладываются отрезки, 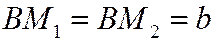 . Написать в полярных координатах уравнение линии (конхоида Никомеда), описываемой точками
. Написать в полярных координатах уравнение линии (конхоида Никомеда), описываемой точками 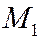 и
и 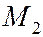 при вращении луча, принимая за полюс точку О, а за полярную ось - перпендикуляр ОА, опущенный из точки О на данную прямую; перейти затем к декартовым координатам, принимая за начало системы точку О, а за ось абсцисс прямую ОА (рис. 71),
при вращении луча, принимая за полюс точку О, а за полярную ось - перпендикуляр ОА, опущенный из точки О на данную прямую; перейти затем к декартовым координатам, принимая за начало системы точку О, а за ось абсцисс прямую ОА (рис. 71),
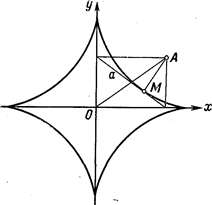 Рис. 70
Рис. 70
|
Отв. 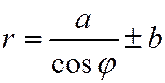 , или
, или 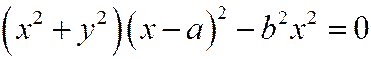 .
.
8. Даны точка О и прямая, находящаяся от точки О на расстоянии ОA=a. Вокруг точки О вращается луч, пересекающий прямую в переменной точке В. На этом луче по обе стороны от точки В откладываются равные отрезки 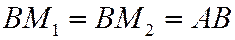 . Составить уравнение линии (строфоида), описываемой точками
. Составить уравнение линии (строфоида), описываемой точками 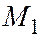 и
и 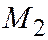 при вращении луча, в полярных координатах, принимая за полюс точку О и за полярную ось перпендикуляр ОА, опущенный из О на данную прямую. Перейти затем к декартовым координатам, принимая за начало координат точку О и за ось абсцисс прямую ОА (рис. 72).
при вращении луча, в полярных координатах, принимая за полюс точку О и за полярную ось перпендикуляр ОА, опущенный из О на данную прямую. Перейти затем к декартовым координатам, принимая за начало координат точку О и за ось абсцисс прямую ОА (рис. 72).
Отв. 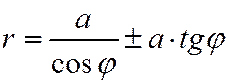 , или
, или  .
.
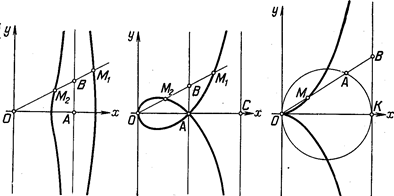
Рис. 71 Рис. 72 Рис. 73
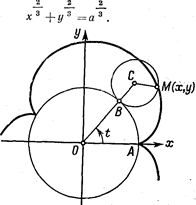
9. На окружности радиуса а взята точка О и через точку K, диаметрально противоположную точке С, к окружности проведена касательная. Вокруг точки О вращается луч, пересекающий окружность и касательную соответственно в точках A и B. На этом луче от точки О откладываем отрезок ОМ, равный отрезку AB луча, заключенному между окружностью и касательной. Линия, описываемая точкой М при вращении луча, называется циссоидой Диоклеса.
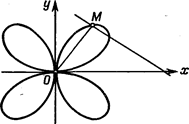
Рис. 74
Написать ее уравнение в полярных координатах, принимая за полюс точку О и за полярную ось диаметр OK Перейти затем к декартовым координатам (рис. 73).
Отв. 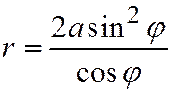 , или
, или 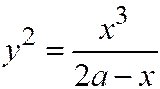 .
.
10. На окружности радиуса а взята точка О и через нее проведен диаметр ОА. Вокруг точки О вращается луч, пересекающий окружность в переменной точке В. На этом луче по обе стороны от точки В откладываются отрезки 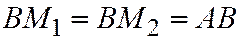 . Написать уравнения линий, описываемых точками
. Написать уравнения линий, описываемых точками 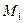 и
и 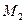 при вращении луча.
при вращении луча.
Отв. Две окружности
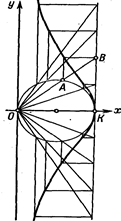
 11. Отрезок постоянной длины 2а скользит своими концами по сторонам прямого угла. Найти линию, описываемую при этом движении отрезка основанием перпендикуляра, опущенного из вершины прямого угла на отрезок (в полярных и декартовых координатах) (рис. 74).
11. Отрезок постоянной длины 2а скользит своими концами по сторонам прямого угла. Найти линию, описываемую при этом движении отрезка основанием перпендикуляра, опущенного из вершины прямого угла на отрезок (в полярных и декартовых координатах) (рис. 74).
Отв. 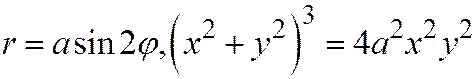 .
.
12. На окружности радиуса а взята точка О. Через точку K, диаметрально противоположную О, к окружности проведена касательная. Вокруг точки О вращается прямая, пересекающая окружность и касательную соответственно в точках A и B. Из точки A проводится прямая, параллельная касательной, а из точки B-прямая, параллельная
Рис.75 Рис.76 диаметру ОК.. Найти геометрическое место точек пересечения этих прямых (верзьера Марии Аньези), принимая за начало прямоугольной системы координат точку О, а за ось абсцисс диаметр ОК (рис. 75).
Отв. 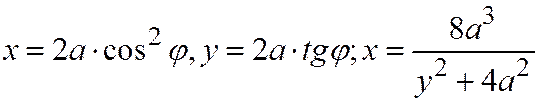 .
.
13. Круг радиуса r катится по кругу радиуса R, оставаясь вне его. Найти параметрические уравнения линии, описываемой точкой катящегося круга (эпициклоида), принимая за начало координат центр неподвижного круга, а за параметр-угол t между положительным направлением оси абсцисс и радиусом неподвижного круга, идущим в точку касания подвижного круга с неподвижным. В начальном положении подвижная окружность касалась неподвижной в точке пересечения последней с осью абсцисс (рис. 76).
Отв. 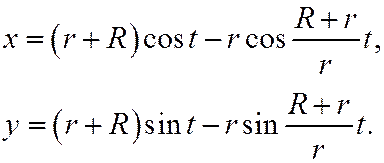
14. Круг радиуса r катится по кругу радиуса R, оставаясь внутри него Написать параметрические уравнения линии, описываемой точкой катящегося круга (гипоциклоида). Выбор системы координат и обозначений такой же как и в предыдущей задаче (рис. 77).
Отв. 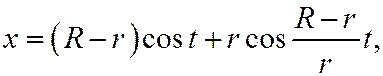
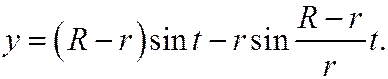
15. Показать, что при R=4r гипоциклоида обращается в астроиду
16. Показать, что при R=2r гипоциклоида обращается в диаметр неподвижного круга
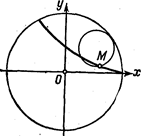 Рис. 77
Рис. 77
|
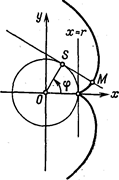 Рис. 78
Рис. 78
|
17. Отрезок постоянной длины движется так, что один его конец скользит по окружности x2+y2=r2, а другой - по оси Ох (шатунно-кривошипный механизм). Составить уравнение кривой, которую описывает точка отрезка разделяющая его на части а и b.
Отв. 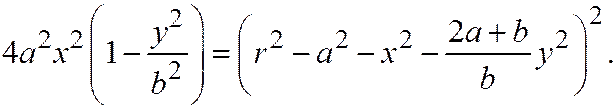
18. По окружности x2+y2=r2 катится прямая, начальное положение которой 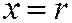 . Определить траекторию точки катящейся прямой, принимая за начальное ее положение точку (r,0) (эвольвента окружности) (рис. 78).
. Определить траекторию точки катящейся прямой, принимая за начальное ее положение точку (r,0) (эвольвента окружности) (рис. 78).
Отв. 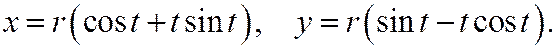
Дата добавления: 2015-08-11; просмотров: 1860;
