Поверхность и ее уравнение.

Уравнением поверхности в общей декартовой или в прямо­угольной системе координат называется уравнение F(х,у,z)=0, которое удовлетворяется координатами любой точки, лежащей на этой поверхности и не удовлетворяется координатами точек, не лежащих на поверхности.

Аналогично определяется уравнение поверхности в сферических координатах 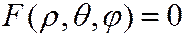(неявное) и в цилиндрических координатах 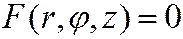(неявное).

В частности, уравнение поверхности в декартовой системе координат может быть задано в виде, разрешенном относительно одной из координат, например в виде z=f(x,y).

Наконец, поверхность может быть задана параметрическими урав­нениями.

Параметрическими уравнениями поверхности П в декартовой системе координат называются уравнения вида

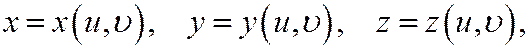
где функции 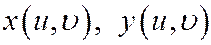и и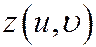меют одну и ту же область определения D (которая представляет собой множество упорядо­ченных пар чисел (и, 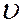); каждой паре чисел (и, 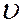) из этой области D соответствует точка M(x(u, 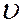), y(u, 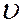), z(и, 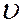)) поверхности П, и для любой точки М поверхности П найдется пара чисел и, 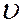из области D, такая, что х(и, 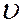), у (и, 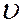), z (и, 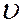) будут координатами точки М. Числа и и 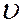называются криволинейными (или внут­ренними) координатами точки М. Аналогично определяются пара­метрические уравнения линии в цилиндрических и сферических координатах.