Поверхности вращения.

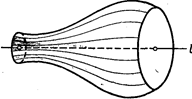 Поверхностью вращения называется поверхность, обладающая следующим свойством: любое ее сечение плоскостью, проходящей через точку поверхности, перпендикулярной к некоторой прямой l (ось вращения), содержит окружность (параллель), центр которой лежит на прямой l и которая проходит через взятую точку.
Поверхностью вращения называется поверхность, обладающая следующим свойством: любое ее сечение плоскостью, проходящей через точку поверхности, перпендикулярной к некоторой прямой l (ось вращения), содержит окружность (параллель), центр которой лежит на прямой l и которая проходит через взятую точку.
Меридианом поверхности вращения называют ее сечение плоскостью, проходящей через ось вращения. Иногда меридианом называют сечение поверхности вращения полуплоскостью, ограниченной осью вращения.
Говорят, что поверхность вращения получается вращением ее меридиана (любого) вокруг оси l (рис. 64).
Теорема. Пусть относительно декартовой прямоугольной системы координат хОу на плоскости задан меридиан С поверхности вращения уравнением
F(x, y)=0. (1)
Тогда уравнение поверхностиП, образованной вращением линии С вокруг оси Ох в декартовой прямоугольной системе координат Oxyz (рис. 65), будет иметь вид
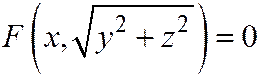 . (2)
. (2)
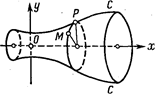
Рис.65
Доказательство. Расстояние от произвольной точки М(х,у,z) пространства до оси Ох равно 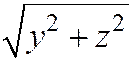 . Поэтому точка М(х,у,z) пространства лежит на поверхности П тогда и только тогда, когда точка Р плоскости хОу с абсциссой х и ординатой
. Поэтому точка М(х,у,z) пространства лежит на поверхности П тогда и только тогда, когда точка Р плоскости хОу с абсциссой х и ординатой 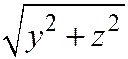 лежит на данном ее меридиане, т. е. тогда и только тогда, когда выполнено соотношение (2).
лежит на данном ее меридиане, т. е. тогда и только тогда, когда выполнено соотношение (2).
Пример 1. Рассмотрим уравнение окружности радиуса а с центром в начале декартовой прямоугольной системы координат хOу. При вращении этой окружности вокруг оси Ох получим сферу радиуса а с центром в начале координат. Уравнение этой сферы на основании предыдущей теоремы имеет вид 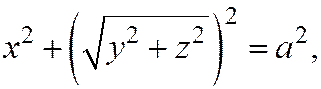 или
или 
Пример 2. Рассмотрим прямую, заданную уравнением y=kx относительно декартовой прямоугольной системы координат.
Уравнение поверхности вращения, полученной при вращении этой прямой вокруг оси Ох, т. е. уравнение прямого кругового конуса с вершиной в начале координат, имеющего своей осью Ох, имеет вид 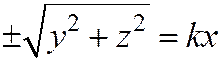 (знак + берется для тех значений х, для которых kx>0, а знак - для тех значений х, для которых kx<0), или
(знак + берется для тех значений х, для которых kx>0, а знак - для тех значений х, для которых kx<0), или 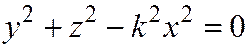 .
.
Тангенс угла а между осью Ох и образующей этого конуса равен 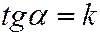 .
.
Пример 3. Рассмотрим прямую, параллельную оси Ох, заданную уравнением 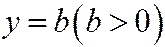 относительно декартовой прямоугольной системы координат. Уравнение поверхности, полученной при вращении этой прямой вокруг оси Ох, т. е. уравнение прямого круглого цилиндра радиуса b, ось которого совпадает с осью Ох, имеет вид
относительно декартовой прямоугольной системы координат. Уравнение поверхности, полученной при вращении этой прямой вокруг оси Ох, т. е. уравнение прямого круглого цилиндра радиуса b, ось которого совпадает с осью Ох, имеет вид
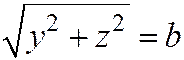 или
или 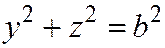 .
.
Пример 4. Рассмотрим окружность радиуса а с центром в точке (0, b), лежащем на оси Оу, заданную уравнением 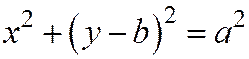 относительно декартовой прямоугольной системы координат.
относительно декартовой прямоугольной системы координат.
Поверхность, полученная вращением этой окружности вокруг оси Ох, имеет уравнение 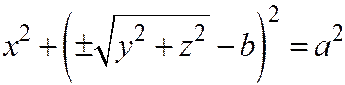 , причем, если b > a > 0, то перед радикалом надо взять только знак +, если -b>а>0, то только знак - . Если
, причем, если b > a > 0, то перед радикалом надо взять только знак +, если -b>а>0, то только знак - . Если  < а, то ±. Упрощая последнее уравнение, получим
< а, то ±. Упрощая последнее уравнение, получим 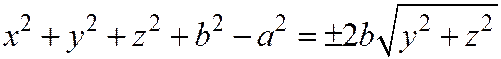 , (1)
, (1)
которое эквивалентно уравнению
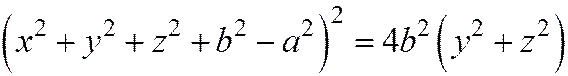 . (2)
. (2)
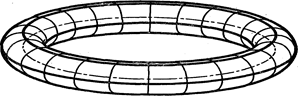
Если b>а>0, то эта поверхность называется тором (рис. 66).
Получим параметрические уравнения этого тора. Пусть С-центр окружности произвольного сечения тора полуплоскостью, проходящей через ось Ox; M(x,y,z) - произвольная точка, лежащая на окружности
|
 |
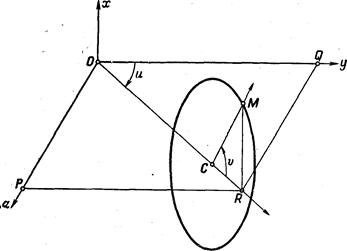 |
(С); R-проекция точки М на плоскость zOу, а Р и Q - проекции точки R на оси Oz и Оу (рис. 67). Обозначим через и угол от оси Оу до оси ОС в плоскости уОz, а через
 - угол от луча
- угол от луча 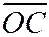 до луча
до луча 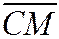 в плоскости СОх (которая ориентирована ориентированным углом
в плоскости СОх (которая ориентирована ориентированным углом  . Тогда:
. Тогда:
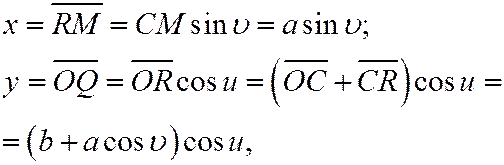
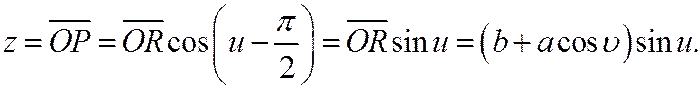 Итак, параметрические уравнения тора:
Итак, параметрические уравнения тора:
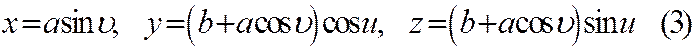 Область D изменения параметров и и
Область D изменения параметров и и  такова:
такова:
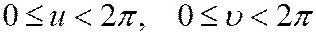 . (D)
. (D)
Параметр и называется долготой точки M тора, а параметр  -широтой. Исключим из уравнений (3) параметры и и
-широтой. Исключим из уравнений (3) параметры и и  . Имеем
. Имеем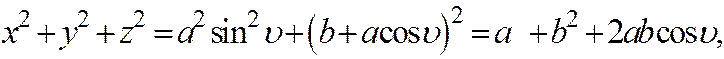 откуда
откуда 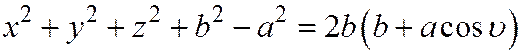 .
.
Далее, 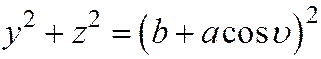 ,
,
значит,
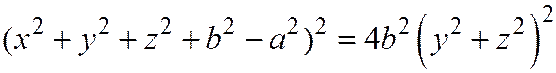
то же уравнение, что и полученное выше.
Дата добавления: 2015-08-11; просмотров: 1227;
