Принцип Даламбера

Если ускорение элементов конструкции известны, то динамическую задачу можно свести к статической. На многочисленных экспериментах, сравнениях и расчетах было показано, что добавление силы инерции к внешним нагрузкам приводит динамическую задачу к обычной статической. То есть, если к внешним силам добавить силы инерции в уравнениях равновесия, то скорости и перемещения, найденные из этих уравнений согласуются с замеренными в эксперименте.

Рассмотрим применение этого принципа на простом примере.

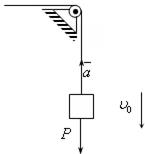
рис.20.5

Пусть груз опускается со скоростью 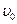. Пусть в результате торможения груз остановился за время 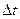. Найдем силу натяжения троса. Пренебрежем силой веса троса и силами ее инерции.

Кроме силы веса груза при торможении появиться сила его инерции:

.

Здесь 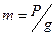- масса груза, а ускорение 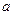вычисляется по формуле:

.

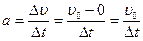Таким образом: .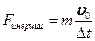

Сила натяжения будет:

.

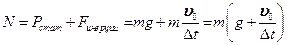Ускорение можно вычислить также и в задачах о вращении тел. Пусть 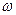- угловая скорость, тогда центростремительное ускорение

.

Следовательно, для этих задач, тоже можно вычислить силу инерции.

В других случаях необходимо решать дифференциальные уравнения вида:

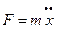. (20.9)

где х – перемещение массы m.