Вынужденные колебания стержня с демпфером
Для тел, которые двигаются в жидкости, Аристотелем был открыт закон, гласящий: чем больше сила, приложенная к телу, тем больше скорость его движения в жидкости.
Для нашего случая схема установки демпферов представлена на левом рисунке 20.12.
Сделаем сечение I-I и рассмотрим верхнюю часть нашего стержня.
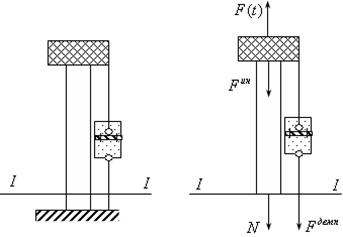
рис.20.12
Выразим 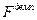 через перемещение груза. Считаем абсолютно жесткими стержни, соединяющие демпфер с грузом и основанием. Тогда перемещение поршня совпадает с перемещением груза.
через перемещение груза. Считаем абсолютно жесткими стержни, соединяющие демпфер с грузом и основанием. Тогда перемещение поршня совпадает с перемещением груза.
Согласно закону движения тела в вязкой жидкости:
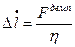 . (20.15)
. (20.15)
где  - коэффициент вязкости. Отсюда:
- коэффициент вязкости. Отсюда:
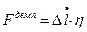 . (20.16)
. (20.16)
Запишем уравнение равновесия верхней части нашего стержня:
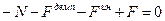
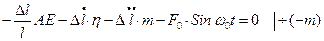
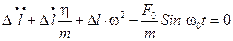 (20.17)
(20.17)
Решение ищем в виде:
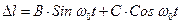 .
.
Подставляя в (20.17), получим:
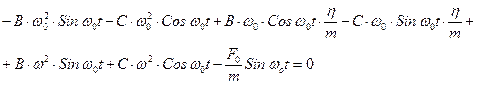
Собирая множители при 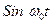 и
и 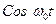 получим:
получим:
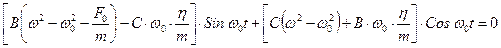 .
.
Чтобы уравнение удовлетворялось в любой момент времени t, квадратные скобки должны быть равны 0:
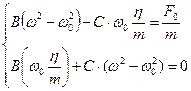
Выразим С из 2-го уравнения:
 . (20.18)
. (20.18)
Подставляя его в первое уравнение, получим:
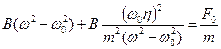 ,
,
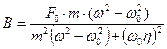 .
.
Из выражения (20.18) находим С:
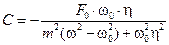
Выводы из решения: Как видно, в знаменателе стоит сумма квадратов двух выражений, следовательно, знаменатель никогда не будет равен 0, таким образом, явления резонанса никогда не будет.
Однако при 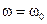 , если вязкость
, если вязкость  демпфера мала, то коэффициент C будет очень большой. Поэтому для того, чтобы перемещения были малы, вязкость демпфера должна быть достаточно велика.
демпфера мала, то коэффициент C будет очень большой. Поэтому для того, чтобы перемещения были малы, вязкость демпфера должна быть достаточно велика.
Примечание: на сегодня масляные демпферы требуют больших затрат по обслуживанию, поэтому ведутся исследования по отысканию податливых конструкционных материалов, которые обладали бы вязкими свойствами, достаточными для демпфирования. Такие свойства материалов называются внутренним трением, им обладают практически все материалы, но в разной степени. Вязкие свойства проявляются в них ярче при высоких температурах.
21. Теория предельного равновесия и её использование при расчете конструкций
Разработчиком современной теории является Гвоздев А.А. В 30-е годы он развивал эту теорию для железобетонных конструкций. В отличие от обычных подходов сопромата эта теория позволяет определить разрушающую нагрузку, а обычные методы работают в области упругого закона.
Основной постулат теории заключается в следующем:
Если в каком то малом элементе тела (стержня), наступает состояние, при котором начинается текучесть, то этот элемент не перестает работать, а продолжает сопротивляться с постоянным напряжением:
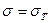 .
.
Разрушением считается состояние не разделения на части, а состояние, при котором происходит переход конструкции в механизм, то есть состояние, при котором она уже деформируется неограниченно и не может удерживать дополнительную нагрузку.
Пример1:
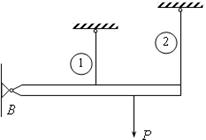
Плита подвешена на двух проволоках. Сколько может выдержать данная конструкция (т.е. необходимо найти разрушающую нагрузку 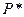 ).
).
Ясно, что плита начнет неограниченно перемещаться (вращаясь около опоры) только тогда, когда оба стержня потекут. Тогда в первом стержне 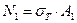 и во втором:
и во втором: 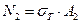 .
.
Введем силовую схему, заменяя противодействие опоры реакциями. Проведем сечение I-I и заменим действие верхней части конструкции на нижнюю силами N1, N2.
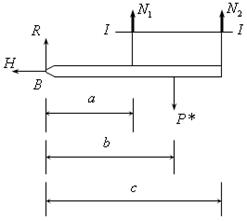
Запишем уравнение равновесия:
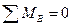
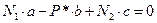
Отсюда получаем разрушающую нагрузку:
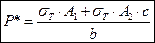 .
.
Дата добавления: 2015-08-11; просмотров: 1289;
