болтовых (заклепочных) и сварных соединений
Пусть 2 элемента соединяются болтом. Существует две опасности – срез болта и сматие пластины или болта.



Разрушение срезом
Считаем, что при разрушении происходит срез болта, ввиду возникновения предельных значений напряжения.
Тогда:
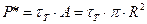 .
.
Если болтов несколько, то получим:
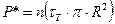 . (21.2)
. (21.2)
Теперь можно найти допустимую силу
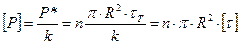 . (21.3)
. (21.3)
Если же дана проектная сила Р , то можно из (21.3) найти количество болтов.
Разрушение смятием
Разрушение может произойти в результате смятия самого болта или пластины. Пластина при этом воздействует на болт по сечению А (см. рисунок) напряжением 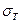 .
.
Тогда:
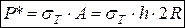
Расчет сварных соединений
Рассмотрим продольные швы:


Нарисуем разрушенное состояние. Из уравнения равновесия следует, что:
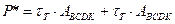 .
.
Запишем условие прочности (здесь k - коэффициент запаса):
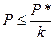 .
.
С учетом того, что 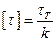 отсюда получаем
отсюда получаем
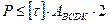 .
.
Основной задачей расчета сварных швов является определение минимально-допустимой длины шва. Выражая площадь фигуры ВСDК через l найдем:
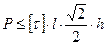 ,
,
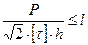 .
.
Это расчетная длина шва. При изготовлении сварки расчетную длину увеличивают на 1 сантиметр, так как по концам шва всегда образуются микротрещины на глубину порядка 0,5 сантиметров.
Торцевые швы (или лобовые швы) рассчитываются совершенно аналогично

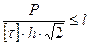
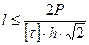
Литература
1. Терегулов И.Г. «Сопротивление материалов и основ теории упругости и пластичности» М.: Высшая школа, 1984
2. Тимошенко С.П. Механика материалов : Учебник для вузов / Гере, Джеймс Монро. - 2-е изд., стер. - СПб. : Лань, 2002. - 672с
3. Работнов Ю.Н. Механика деформируемого твердого тела. – М.: Наука, 1988. – 712с.
4. Феодосьев В.И. Сопротивление материалов : Учебник для вузов / 11-е изд., стереотип. - М. : МГТУ им.Н.Э.Баумана, 1999. - 592с.
5. Александров А.В., Потапов В.Д., Державин Б.П. Сопротивление материалов. – М.: «Высшая школа», 2000. – 560с.
6. Беляев Н.М. Сопротивление материалов. -М.: Изд-во «Наука», 1976. – 607с.
7. Варданян Г.С., Андреев В.И., Атаров Н.М., Горшков А.А. Сопротивление материалов с основами теории упругости и пластичности. – М.: Изд-во АСВ, 1995. – 568с.
8. Варданян Г.С., Атаров Н.М., Горшков А.А. Сопротивление материалов. – М.: Инфра – М., 2003. – 478с.
9. Дарков А.В., Шпиро Г.С. Сопротивление материалов. -М.: «Высшая школа», 1989. – 624с.
10. Долинский Ф.В., Михайлов М.Н. Краткий курс сопротивления материалов. – М.: «Высшая школа», 1988. – 431с.
11. Копнов В.А., Кривошапко С.Н. Сопротивление материалов. Руководство для решения задач и выполнения расчетно-графических работ. – М.: «Высшая школа», 2005. – 351с.
12. Кочетов В.Т., Кочетов М.В., Павленко А.Д. Сопротивление материалов. – СПб.: БХВ – Петербург, 2004. – 544с.
13. Костенко Н.А., Балясникова С.В., Волошановская Ю.Э. Сопротивление материалов. – М.: «Высшая школа», 2000. – 430с.
14. Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. – Киев: «Наук.думка», 1988. – 736с.
15. Сопротивление материалов /Под редакцией Смирнова А.Ф./ М.: «Высшая школа», 1975. – 480с.
16. Строительная механика. Под редакцией Даркова А.В. - М.: «Высшая школа», 1976. – 600с.
17. Степин П.А. Сопротивление материалов. – М.: «Высшая школа», 1988. – 366с.
18. Серазутдинов М.Н., Островская Э.Н., Петухов Н.П., Сидорин С.Г. Механика. Вопросы теоретической механики, сопротивления материалов, деталей машин. Казань: Центр инновационных технологий, 2007. – 330с.
СОДЕРЖАНИЕ
| Введение | ||
| 1. | Геометрические характеристики сечений | |
| 1.1. Статический момент фигуры | ||
| 1.2. Моменты второго порядка | ||
| 1.2.1. Осевой момент инерции | ||
| 1.2.2. Центробежный момент площади | ||
| 1.2.3. Свойства симметричных фигур | ||
| 1.2.4. Геометрический и механический смысл моментов | ||
| 1.2.5. Формулы для вычисления моментов инерции канонических фигур | ||
| 1.2.5.1. Формулы для вычисления моментов инерции прямоугольника относительно центральных осей | ||
| 1.2.5.2. Формула для вычисления момента инерции окружности относительно центральных осей | ||
| 1.2.5.3. Формула для вычисления момента инерции треугольника | ||
| 1.2.6. Связь моментов относительно разных осей | ||
| 1.2.6.1. Связь моментов относительно параллельных осей | ||
| 1.2.6.2. Связь моментов относительно повернутых осей | ||
| 1.2.6.3. Главные оси и главные моменты | ||
| 2. | Основные понятия и закономерности сопромата | |
| 2.1. Расчетная схема | ||
| 2.1.1. Условия закрепления | ||
| 2.1.2. Внешние силовые факторы | ||
| 2.2. Усилие растяжения (сжатия) | ||
| 2.3. Метод сечений | ||
| 2.4. Нормальное напряжение | ||
2.5. Закон равномерного распределения нормального напряжения 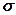 при растяжение (сжатие) при растяжение (сжатие)
| ||
| 2.6. Предел прочности | ||
| 2.7. Условие прочности | ||
| 3. | Внутренние силовые факторы (ВСФ) | |
| 3.1. Случай воздействия внешних сил в одной плоскости | ||
3.2. Основные соотношения между погонной силой q, поперечной силой 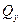 и изгибающим моментом и изгибающим моментом
| ||
| 4. | Эпюры ВСФ | |
| 5. | Правила контроля построения эпюр | |
| 6. | Общий случай напряженного состояния | |
| 6.1. Нормальные и касательные напряжения | ||
| 6.2. Закон парности касательных напряжений | ||
| 7. | Деформации |
| 8. | Основные предположения и законы, используемые в сопротивлении материалов | |
| 8.1. Основные предположения, используемые в сопротивлении материалов | ||
| 8.2. Основные законы, используемые в сопротивлении материалов | ||
| 9. | Примеры использования законов механики при расчете строительных сооружений | |
| 9.1. Расчет статически неопределимых систем | ||
| 9.1.1. Статически неопределимая железобетонная колонна | ||
| 9.1.2. Температурные напряжения | ||
| 9.1.3. Монтажные напряжения | ||
| 9.1.4. Расчет колонны по теории предельного равновесия | ||
| 9.2. Особенности температурных и монтажных напряжений | ||
| 9.2.1. Независимость температурных напряжений от размеров тела | ||
| 9.2.2. Независимость монтажных напряжений от размеров тела | ||
| 9.2.3. О температурных и монтажных напряжениях в статически определимых системах | ||
| 9.3. Независимость предельной нагрузки от самоуравновешенных начальных напряжений | ||
| 9.4. Некоторые особенности деформирования стержней при растяжении и сжатии с учетом силы тяжести | ||
| 9.5. Расчет элементов конструкций с трещинами | ||
| 9.6. Расчет конструкций на долговечность | ||
| 9.6.1. Долговечность железобетонной колонны при наличии ползучести бетона | ||
| 9.6.2. Условие независимости напряжений от времени в конструкциях из вязкоупругих материалов | ||
| 9.7. Теория накопления микроповреждений | ||
| 10. | Расчет стержней и стержневых систем на жесткость | |
| 10.1. Формула Мора для вычисления перемещения конструкции | ||
| 10.2. Формула Мора для стержневых систем | ||
| 11. | Закономерности разрушения материала | |
| 11.1. Закономерности сложного напряженного состояния | ||
11.2. Зависимость 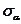 и и 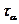 от касательных напряжений от касательных напряжений
| ||
| 11.3. Главные напряжения | ||
| 11.4. Виды разрушений материалов | ||
| 11.5. Теории кратковременной прочности | ||
| 11.5.1. Первая теория прочности | ||
| 11.5.2. Вторая теория прочности | ||
| 11.5.3. Третья теория прочности (теория максимальных касательных напряжений) | ||
| 11.5.4. Четвертая теория (энергетическая) | ||
| 11.5.5. Пятая теория – критерий Мора | ||
| 11.5.6. Краткое изложение теории прочности | ||
| 12. | Краткое изложение теорий прочности в задачах сопротивления материалов. | |
| 13. | Расчет цилиндрической оболочки под воздействием внутреннего давления | |
| 14. | Усталостное разрушение (циклическая прочность) | |
| 14.1. Расчет сооружений при циклическом нагружении с помощью диаграммы Велера | ||
| 14.2. Расчет сооружений при циклическом нагружении по теории развивающихся трещин | ||
| 15. | Изгиб балок | |
| 15.1 Нормальные напряжения. Формула Навье | ||
| 15.2. Определение положения нейтральной линии (оси х) в сечении | ||
| 15.3 Момент сопротивления | ||
| 15.4. Ошибка Галилея | ||
| 15.5. Касательные напряжения в балке | ||
| 15.6. Касательные напряжения в полке двутавра | ||
| 15.7. Анализ формул для напряжений | ||
| 15.8. Эффект Эмерсона | ||
| 15.9. Парадоксы формулы Журавского | ||
| 15.10. О максимальных касательных напряжениях (τzy )max | ||
| 15.11. Расчеты балки на прочность | ||
| 16. | Расчет балки на жесткость | |
| 16.1. Формула Мора для вычисления прогиба | ||
| 16.1.1. Методы вычисления интегралов. Формулы трапеций и Симпсона | ||
| 16.2. Вычисление прогибов на основе решения дифференциального уравнения изогнутой оси балки | ||
| 16.2.1. Решение дифференциального уравнения изогнутой оси балки | ||
| 16.2.2. Правила Клебша | ||
| 16.2.3. Условия для определения С и D | ||
| 16.2.4. Балки на упругом основании. Закон Винклера | ||
| 16.4. Уравнение изогнутой оси балки на упругом основании | ||
| 16.5. Бесконечная балка на упругом основании | ||
| 17. | Потеря устойчивости | |
| 17.1. Формула Эйлера | ||
| 17.2. Другие условия закрепления | ||
| 17.3. Предельная гибкость. Длинный стержень | ||
| 17.4. Формула Ясинского | ||
| 17.5. Продольный изгиб | ||
| 18. | Кручение валов | |
| 18.1. Кручение круглых валов | ||
| 18.2. Напряжения в сечениях вала | ||
| 18.3. Расчет вала на жесткость | ||
| 18.4. Свободное кручение тонкостенных стержней | ||
| 18.5. Напряжения при свободном кручении тонкостенных стержней замкнутого профиля | ||
| 18.6. Угол закрутки тонкостенных стержней замкнутого профиля | ||
| 18.7. Кручение стержней открытого профиля | ||
| 19. | Сложная деформация. | |
| 19.1. Эпюры внутренних силовых факторов (ВСФ) | ||
| 19.2. Растяжение с изгибом | ||
| 19.3. Максимальные напряжения при растяжении с изгибом | ||
| 19.4. Косой изгиб | ||
| 19.5. Проверка прочности круглых стержней при кручении с изгибом. | ||
| 19.6. Внецентренное сжатие. Ядро сечения | ||
| 19.7. Построение ядра сечения | ||
| 20. | Динамические задачи | |
| 20.1. Удар | ||
| 20.2. Область применения формулы для коэффициента динамичности | ||
| 20.3. Выражение коэффициента динамичности через скорость ударяющего тела | ||
| 20.4. Принцип Даламбера | ||
| 20.5. Колебания упругих стержней | ||
| 20.5.1. Свободные колебания | ||
| 20.5.2. Вынужденные колебания | ||
| 20.5.3. Вынужденные колебания стержня с демпфером | ||
| 21. | Теория предельного равновесия и её использование при расчете конструкций | |
| 21.1. Задача изгиба балки | ||
| 21.2. Применение теории предельного равновесия для расчета болтовых (заклепочных) и сварных соединений | ||
| Литература |
Дата добавления: 2015-08-11; просмотров: 1412;
