Закон Ампера. Движение заряженных частиц в магнитном поле

Закон Ампера: на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля

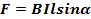(11)

где α – угол между направлением тока и индукцией магнитного поля.

Формула (11) справедлива для прямолинейного проводника и однородного поля.

Если проводник имеет произвольную форму и поле неоднородно то выражение (11) примет вид

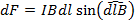(12)

или

. (13)

где dl – малый участок проводника, имеющий направление, совпадающее с направлением тока.

Произведение 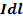называют элементом тока.

Для определения направление силы, действующей на проводник с током, помещенный в магнитное поле, применяют правило левой руки: если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а вытянутые четыре пальца совпадали с направлением тока в проводнике, то отогнутый большой палец укажет направление силы Ампера (рис.8).

Рис.8.

Сила Лоренца. Магнитное поле действует не только на проводники с то­ком, но и на отдельные за­ряды, движущиеся в магнитном поле.

Сила, действующая на электрический за­ряд q, движущийся в магнитном поле со скоростью v, называется силой Лорен­ца

F= 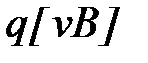(14)

где В — индукция магнитного поля, в ко­тором заряд движется.

· · · · ·

В

· · · · ·

v

· · · · ·

· · · · ·

F

· · · · ·

Рис.9

Направление силы Лоренца определя­ется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль векто­ра v (для q > 0 направления I и v совпадают, для q < 0 — противоположны), то отогнутый большой палец покажет направление силы, действующей на поло­жительный заряд.

На рис.9 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд, движущийся в том же направлении и магнитном поле, сила действует в противоположном на­правлении. Модуль силы Лоренца равен

F = qvB sin 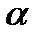, (15)

где 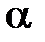— угол между v и В.

Отметим еще раз, что маг­нитное поле не действует на покоящий­ся электрический заряд. В этом сущест­венное отличие магнитного поля от элект­рического. Магнитное поле действует только на движущиеся в нем заряды.

Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Ло­ренца может быть использовано для определения вектора магнитной индукции В.

Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы. поэтому она изменяет только направле­ние этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменя­ется.

Если на движущийся электрический за­ряд помимо магнитного поля с индукци­ей В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действую­щей со стороны электрического поля, и силы Лоренца:

F = qE + q [vB]. (16)

Это выражение называется формулой Лоренца.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F = q [vB] постоянна по модулю и нор­мальна к траектории частицы. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определя­ется из условия

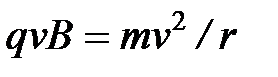
Период вращения частицы, т. е. время Т, затрачиваемое ею на один полный оборот

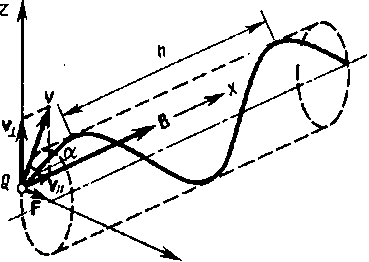
Рис.10

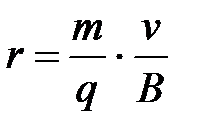(17)

Подставив выражение (24.1) в предыдущее, получим

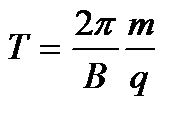(18)

т. е. период вращения частицы в одно­родном магнитном поле определяется только величиной, обратной удельному заряду (q/m) частицы, и магнитной индукцией поля, но не зависит от ее ско­рости (при 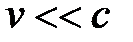). На этом основано действие циклических ускорителей заря­женных частиц.

Если скорость v заряженной частицы направлена под углом и к вектору В (рис.10), то ее движение можно пред­ставить в виде суперпозиции: 1) равно­мерного прямолинейного движения вдоль поля со скоростью v = 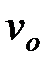cos 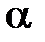2) равно­мерного движения со скоростью v=vsin 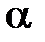по окружности в плоскости, пер­пендикулярной полю. Радиус окружности определяется формулой (24.1) (в данном случае надо заменить v на v = v sin 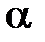). В результате сложения обоих движений возникает движение по спирали, ось ко­торой параллельна магнитному полю (см. рис.10). Шаг винтовой линии

h = vïïТ = vTcos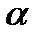

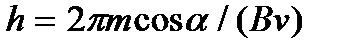(19)

Направление, в котором закручивается спираль, зависит от знака заряда частицы.