Закон Био-Савара-Лапласа и его применение. Магнитное поле постоянных токов раз­личной формы изучалось французскими учеными Ж

Магнитное поле постоянных токов раз­личной формы изучалось французскими учеными Ж. Био (1774-1862) и Ф. Саваром (1791-1841). Результаты этих опытов были обобщены выдающимся француз­ским математиком и физиком П. Лапласом.

Закон Био - Савара - Лапласа для про­водника с током I, элемент которого d 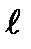создает в некоторой точке А (рис.2) индукцию поля dB, записывается в виде

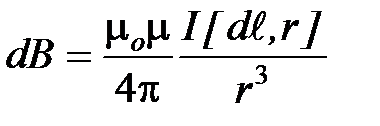. (5)

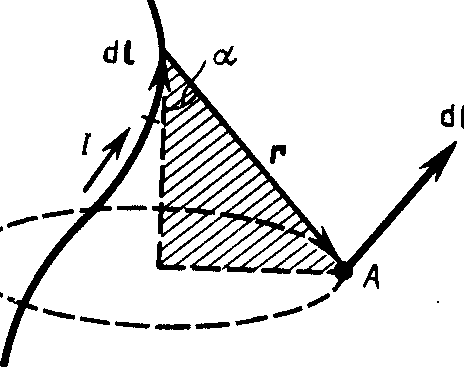
Рис. 2

Направление dB перпендикулярно dl и r, т. е. перпендикулярно плоскости, в которой они лежат, и совпадает с касатель­ной к линии магнитной индукции. Это направление может быть найдено по пра­вилу нахождения линий магнитной индук­ции (правилу правого винта): направление вращения головки винта дает направление dB, если поступательное движение бурав­чика соответствует направлению тока в элементе.

Модуль вектора dB определяется выра­жением

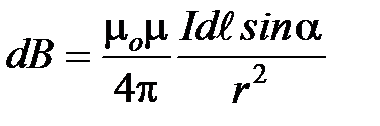, (6)

где 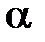— угол между векторами dl и г;

dB — магнитная индукция поля, созда­ваемого элементом проводника длиной d 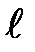. Интегрирование производится по всей длине проводника .

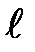Расчет характеристик магнитного поля (В и Н) по приведенным формулам в об­щем случае довольно сложен. Однако если распределение тока имеет определен­ную симметрию, то применение закона Био - Савара - Лапласа совместно с принципом суперпозиции позволяет до­вольно просто рассчитать конкретные поля. Рассмотрим два примера.

Магнитное поле прямого тока — тока, текущего по тонкому прямому проводу бесконечной длины (рис.3). В произ­вольной точке А, удаленной от оси про­водника на

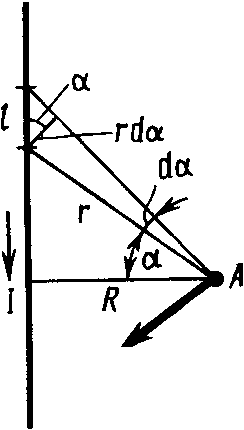
Рис. 3

расстояние R, векторы dB от всех элементов тока имеют одинаковое направление, перпендикулярное плоскости чертежа. Поэтому сложение векторов dB можно заменить сложением их модулей. В качестве постоянной интегрирования выберем угол 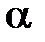, выразив через него все остальные величины. Из рис.3 следует, что

.

Подставив эти выражения в (5), по­лучим, что магнитная индукция, созда­ваемая одним элементом проводника, равна

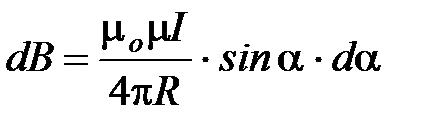(7)

Так как угол 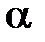для всех элементов пря­мого тока изменяется в пределах от 0 до 180° , то, согласно (6) и (7),

.

Следовательно, магнитная индукция поля прямого тока

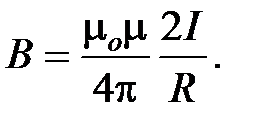(8)

Магнитное ноле в центре кругового проводника с током (рис.4). Как следует из рисунка, все элементы кругового про­водника с током создают в центре маг­нитное поле одинакового направления - вдоль нормали от витка. Поэтому сло­жение векторов dB можно заменить сло­жением их модулей.

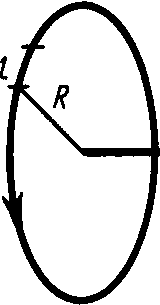
Рис. 4

Так как все элемен­ты проводника перпендикулярны радиусу-вектору (sin 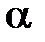=1) и расстояние всех эле­ментов проводника до центра кругового тока одинаково и равно R, то, согласно (7),

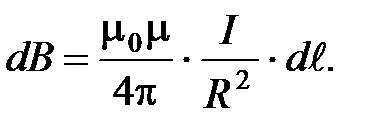
Тогда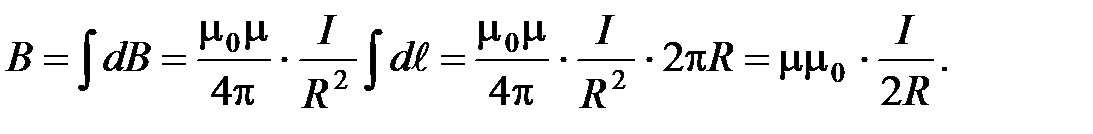

Следовательно, магнитная индукция поля в центре кругового проводника с током

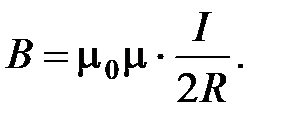(9)

Так как магнитное поле является силовым, то его, по аналогии с электрическим изображают с помощьюлиний магнитной индукции .

Линии индукции можно “проявить” с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам. Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от силовых линий электростатического поля, которые являются разомкнутыми, начинаясь на положительных зарядах и кончаясь на отрицательных. Поле, обладающее замкнутыми силовыми линиями, называется вихревым. Направление силовой линии совпадает с направлением вектора индукции и может быть определено по правилу правого винта (буравчика): если вворачивать буравчик с правой резьбой по направлению тока в проводнике, то направление движения рукоятки буравчика укажет направление линий магнитной индукции (см. рис. 5,6,7).

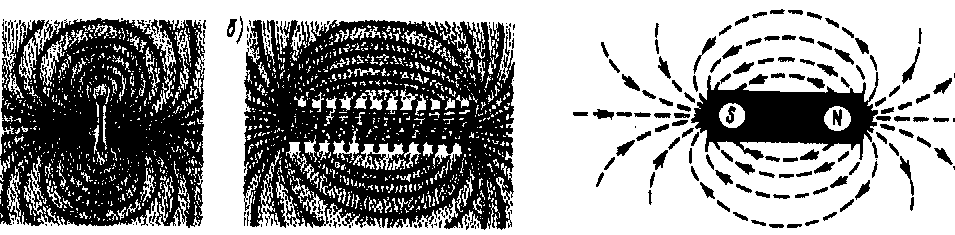
Рис.5. Рис.6. Рис.7.

Для магнитного поля, как и для электрического, справед­лив принцип суперпозиции: магнитное поле, создаваемое несколькими токами или движущимися зарядами, равно век­торной сумме магнитных полей, создавае­мых каждым током или движущимся зарядом в отдельности.

Так, в соответ­ствии с принципом суперпозиции маг­нитная индукция В в произвольной точ­ке магнитного поля проводника с током I равна

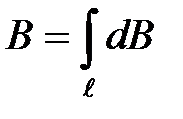. (10)