Закон Ома. Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т.е
Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению на концах проводника:
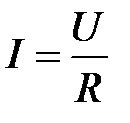 , (6)
, (6)
где R – электрическое сопротивление проводника.
Уравнение (6) выражает закон Ома для участка цепи (не содержащего источника тока): сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Физическая единица измерения сопротивления – ом (Ом): 1Ом – сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток силой 1А.
Сопротивление проводников зависит от его размеров и формы, а также материала, из которого проводник изготовлен. Для цилиндрического проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:
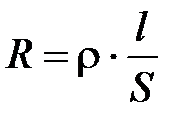 , (7)
, (7)
где r - коэффициент пропорциональности, характеризующий материал проводника. Он называется удельным электрическим сопротивлением. Единица измерения – (Ом×м).
Наименьшим удельным сопротивлением обладают серебро и медь (1,6×10-8Ом×м и 1,7×10-8Ом×м). Закон Ома можно представить в дифференциальной форме. Подставив выражение (7) в (6), получим
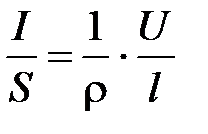 , (8)
, (8)
где 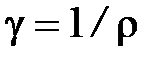 - удельная электрическая проводимость вещества проводника. Ее единица (См/м).
- удельная электрическая проводимость вещества проводника. Ее единица (См/м).
Учитывая, что  - напряженность электрического поля в проводнике,
- напряженность электрического поля в проводнике, 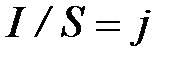 - плотность тока, то формулу (8) можно записать в виде
- плотность тока, то формулу (8) можно записать в виде
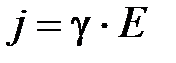 . (9)
. (9)
Так как носители заряда в каждой точке движутся в направлении вектора Е, то направления j и E совпадают. Поэтому формулу (9)можно записать в векторной форме
j = g×E. (10)
Выражение (10) – закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в той же точке. Это соотношение справедливо и для переменных полей.
При последовательном соединении проводников их сопротивления складываются
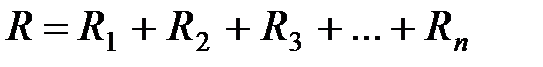 .
.
Дата добавления: 2015-08-11; просмотров: 1142;
