Существования экстремумов

Как и в случае функции одной переменной, возникает задача о нахождении необходимых и достаточных условий существования экстремумов. Сформулируем их для функций двух независимых переменных.

Пусть 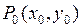– точка локального экстремума для функции 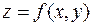. Зафиксируем значение одной переменной 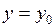. Тогда функция 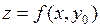является функцией одной переменной 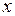, а – ее точка экстремума. По необходимому признаку для функции одной переменной производная в этой точке равна нулю или не существует, т. е. 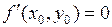или не существует. Для функции 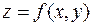это условие, очевидно, означает, что в точке экстремума частная производная по 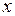равна нулю или не существует. Аналогичные рассуждения можно провести для другой переменной. Таким образом, получаем следующие необходимые условия существования экстремума.

Теорема 1(необходимые условия существования экстремума)

Если функция 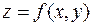в точке 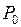имеет экстремум, то в этой точке обе частные производные равны нулю ( 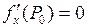, ) или, по крайней мере, одна из них не существует.

Теорема 1 имеет простой геометрический смысл. Касательная плоскость к поверхности 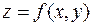в точке экстремума 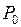параллельна плоскости 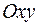( 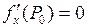, ) или не существует.

Необходимые условия существования экстремума остаются справедливыми и для функций большего числа переменных.

Точки, в которых все частные производные первого порядка функции 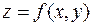равны нулю или хотя бы одна из них не существует, называются критическими точками.

Если в критической точке функция дифференцируема, то все частные производные первого порядка в ней обращаются в нуль. Такую точку часто называют стационарной.

Другая форма необходимых условий локального экстремума. Если функция 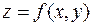дифференцируема в точке 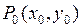и имеет в этой точке локальный экстремум, то .

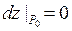Для отыскания стационарных точек функции 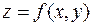находят частные производные первого порядка и решают систему уравнений

(1)

Пример 1.Найти стационарные точки функции .

Решение. Находим частные производные первого порядка и составляем систему уравнений (1):

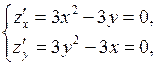или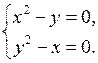

Решив эту систему, получим две стационарные точк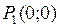и и .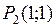

Согласно теореме 1 любая точка экстремума является критической точкой функции, но не всякая критическая точка является точкой экстремума, т. е. необходимые условия (теорема 1) не являются достаточными условиями существования экстремума.

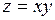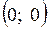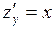Действительно, для функции точка является критической, так как в ней частные производные и обращаются в нуль. Однако в этой точке функция не имеет экстремума, поскольку в точке 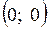функция равна нулю, а в любой окрестности данной точки она принимает как положительные, так и отрицательные значения. Следовательно, не существует окрестности точки 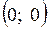, где приращение функции сохраняет знак.

Ответ на вопрос, является ли стационарная точка точкой экстремума, дают достаточные условия существования экстремума, которые будут сформулированы ниже в виде теоремы.

Теорема 2 (достаточные условия существования экстремума).

Пусть функция 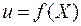, где , дважды непрерывно дифференцируема в окрестности стационарной точки 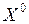. Тогда точка :

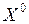1) является точкой строгого минимума функции, если . Причем равенство имеет место только при условии .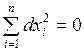

2) является точкой строгого максимума функции, если .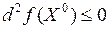

3) не является точкой экстремума функции, если 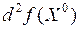принимает как положительные, так и отрицательные значения.

Эти условия не являются необходимыми. Например, функция 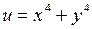имеет в точке 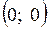строгий минимум, хотя 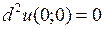при любых 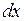и .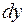

Определение. Функция вида , где 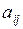– постоянные вещественные числа, называется квадратичной формой от переменных 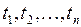, а числа 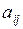– её коэффициентами.

Замечание.Если аргументы 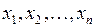являются независимыми переменными, то второй дифференциал дважды непрерывно дифференцируемой в данной точке 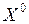функции 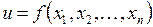представляют собой симметричную квадратичную форму от переменных 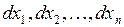. Коэффициенты этой формы равны соответствующим частным производным второго порядка, взятым в точке .

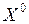Достаточные условия 1), 2), 3) означают соответственно, что квадратичная форма 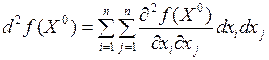положительно определенная, отрицательно определенная и неопределенная.

Будем рассматривать матрицу квадратичной формы (матрицу Гессе)

(1)