Критерий Сильвестра.
1. Квадратичная форма положительно определена, если все главные миноры матрицы (1) являются положительными. В этом случае в точке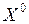 
– минимум.
2. Квадратичная форма отрицательно определена, если все главные миноры нечетного порядка являются отрицательными, а четного порядка – положительными. В этом случае в точке 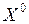– максимум.
В частном случае функции двух переменных достаточные условия существования строгого экстремума можно сформулировать следующим образом.
Теорема 2* (достаточные условия существования экстремума функции двух переменных)
Пусть функция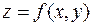 
в стационарной точке 
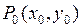имеет непрерывные частные производные до второго порядка включительно. Если 
, 
, 
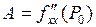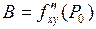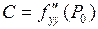и 
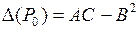, то возможны три случая:
1) при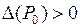 
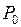– точка экстремума, причем, в точке 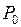максимум, когда 
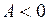, и минимум, когда 
;
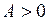2) при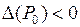 
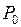не является точкой экстремума;
3) при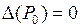 
о характере стационарной точки 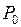никакого заключения сделать нельзя, нужны дополнительные исследования.
Пример 2.Исследовать на экстремум функцию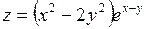 
.
Решение. Найдем стационарные точки функции. Для этого вычислим первые частные производные:
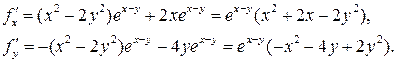
Приравнивая их к нулю, получим систему
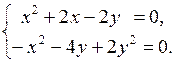
Решениями системы являются две стационарные точк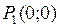и: 
и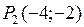 
. Для выяснения их характера согласно теореме 2* найдем 
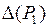и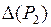 
, вычислив предварительно значения частных производных второго порядка.
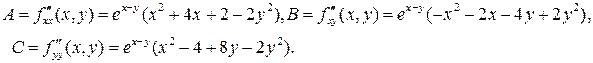
Для точки 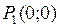имеем 
, 
, 
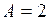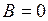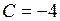и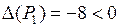 
. На основании теоремы 2* делаем вывод, что в точке 
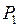функция экстремума не имеет. Для точки 
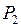соответственно получаем
, 
, 
, 
.
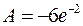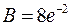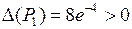Следовательно 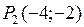–точка экстремума, а поскольку 
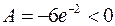, то 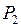– точка максимума и максимальное значение функции 
.
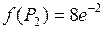Пример 3.Найти локальные экстремумы функции
.
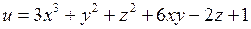Дата добавления: 2015-08-11; просмотров: 1772;