В замкнутой области.
Лекция № 8
Наибольшее и наименьшее значения функции
в замкнутой области.
Определение.Точка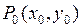 
называется точкой максимума функции 
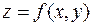, а значение 
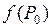– максимумом (максимальным значением), если существует окрестность точки 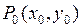, для всех точек 
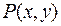которой, отличных от точки 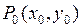, выполняется неравенство 
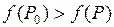. (1)
Определение.Точка 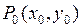называется точкой минимума функции 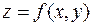, а значение 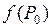– минимумом (минимальным значением), если существует окрестность точки 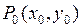, для всех точек 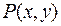которой, отличных от точки 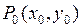, выполняется неравенство 
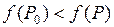. (2)
Точки максимума и минимума функции 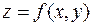называются экстремальными точками, или экстремумами, а значения функции в этих точках экстремальными значениями.
Из неравенств (1) и (2) следует, что в точке экстремума 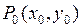полное приращение функции 
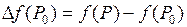сохраняет определенный знак в некоторой окрестности этой точки, причем 
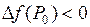, если 
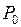– точка максимума, и 
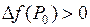, если 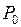– точка минимума.
Отметим, что понятия экстремумов - локальные понятия. Если, например, 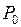– точка максимума, то 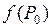является наибольшим значением в некоторой окрестности точки 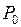, но может не быть таковым во всей области 
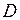, т. е. вне указанной окрестности могут существовать точки, в которых значения функции будут больше, чем значение в точке 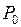. В связи с этим точки экстремумов часто называют точками локального экстремума.
Если неравенство (1) (или (2)) справедливо для всех точек области 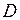, то говорят, что в точке 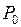, функция достигает наибольшего (или наименьшего) значения в области 
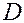. Точки локального экстремума не следует смешивать с точками, в которых функция достигает наибольшего и наименьшего значения.
Дата добавления: 2015-08-11; просмотров: 765;