Закон Ома для замкнутой цепи

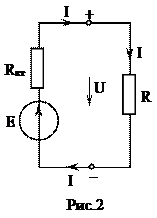На рисунке 2 показана простейшая замкнутая цепь, состоящая из реального источника э.д.с. Е, имеющего внутреннее сопротивление R_вт и нагрузочного резистора с сопротивлением R (сопротивление соединительных проводов включено в сопротивление R резистора).

Закон Ома для замкнутой цепи формулируется следующим образом: сила тока (ток, величина тока) прямо пропорциональна электродвижущей силе (э.д.с.) источника и записывается в виде:

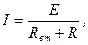
где 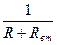– коэффициент пропорциональности.

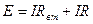
и введем обозначение U = IR – напряжение на выходных зажимах источника э.д.с. (генератора), которое одновременно является падением напряжения, создаваемым током I на внешнем сопротивлении R нагрузочного резистора.

,

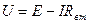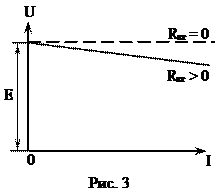которая представляет собой аналитическое выражение внешней характеристики источника э.д.с. Эту зависимость можно сокращенно записать в виде U = F(I) при E = const, R_вт = const. Внешней характеристикой принято называть графическую зависимость U = F(I), показанную на рисунке 3.

Сплошной линией показана внешняя характеристика реального источника э.д.с., в котором с ростом тока I увеличивается падение напряжения на внутреннем сопротивлении IR_вт, в результате чего с ростом тока выходное напряжение источника U уменьшается. Пунктирной линией на рисунке 3 показана внешняя характеристика идеального источника э.д.с., у которого отсутствует внутреннее сопротивление (R_вт = 0), а, следовательно, и внутреннее падение напряжения (IR_вт = 0). В результате равенство (5) принимает вид

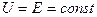и характеристика представляет собой горизонтальную линию. Такой идеальный источник называют источником (генератором) бесконечной мощности, поскольку он гарантирует постоянство напряжения при сколь угодно больших токах нагрузки.