Пример 1. а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка
а) Англо-русский словарь устанавливает соответствие между множествами слов русского и английского языка. Оно не является функциональным, так как почти каждому русскому слову соответствует несколько английских переводов; оно, также, не является, как правило, полностью определённым соответствием, так как всегда существуют английские слова, не включённые в данный словарь. Таким образом, это частичное соответствие.
б) Соответствие между аргументами функции 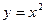 и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции
и значениями этой функции является функциональным. Однако оно не является взаимнооднозначным, так как каждому значению функции 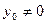 соответствуют два прообраза
соответствуют два прообраза 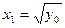 и
и 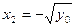 .
.
в) Соответствие между расположенными на шахматной доске фигурами и занимаемыми ими полями является взаимно однозначным.
г) Соответствие между телефонами города Вязьмы и их пятизначными номерами обладает, на первый взгляд, всеми свойствами взаимнооднозначного соответствия. Однако оно, например, не сюръективно, поскольку существуют пятизначные числа, не соответствующие никаким телефонам.
2. Взаимнооднозначные соответствия и мощности множеств.
Если между двумя конечными множествами А и В существует взаимнооднозначное соответствие, то эти множества равномощны. Этот очевидный факт позволяет, во-первых, установить равенство мощности этих множеств, не вычисляя их. Во-вторых, часто можно вычислить мощность множества, установив его однозначное соответствие с множеством, мощность которого известна, либо легко вычисляется.
Теорема 2.1. Если мощность конечного множества А равна 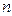 , то число всех подмножеств А равно
, то число всех подмножеств А равно 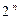 , то есть
, то есть  .
.
Множество всех подмножеств множества М называется булеаном и обозначается 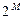 . Для конечных множеств выполняется:
. Для конечных множеств выполняется: 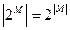 .
.
Определение. Множества А и В называются равномощными, если между их элементами можно установить взаимнооднозначное соответствие.
Заметим, что для конечных множеств это утверждение легко доказать. Для бесконечных множеств оно определят само понятие равномощности.
Определение. Множество А называется счётным, если оно равномощно множеству натуральных чисел 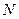 :
: 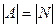 .
.
Очень упрощённо можно сказать, что данное бесконечное множество является счётным, если для его элементов можно установить нумерацию с помощью натуральных чисел.
Без доказательства примем ряд важных фактов:
1. Любое бесконечное подмножество множества натуральных чисел является счётным.
2. Множество  является счётным.
является счётным.
3. Множество рациональных чисел  является счётным (является следствием из предыдущего утверждения).
является счётным (является следствием из предыдущего утверждения).
4. Объединение конечного числа счётных множеств является счётным.
5. Объединение счётного числа конечных множеств является счётным.
6. Объединение счётного числа счётных множеств является счётным.
Все эти утверждения, как можно видеть, позволяют достаточно успешно устанавливать факт, что данное множество является счётным. Однако сейчас будет показано, что не всякое бесконечное множества является счётным; существует множества большей мощности.
Теорема 2.2 (теорема Кантора). Множество всех действительных чисел из отрезка 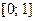 не является счётным.
не является счётным.
Доказательство. Допустим, что множество 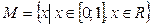 является счётным и существует его нумерация. Поскольку любое действительное число можно представить в виде бесконечной десятичной дроби (периодической или непериодической), то проделаем это с числами данного множества. Расположим их в порядке этой нумерации:
является счётным и существует его нумерация. Поскольку любое действительное число можно представить в виде бесконечной десятичной дроби (периодической или непериодической), то проделаем это с числами данного множества. Расположим их в порядке этой нумерации:
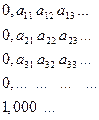
Теперь рассмотрим любую бесконечную десятичную дробь вида 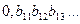 , организованную таким образом, что
, организованную таким образом, что 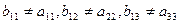 и так далее. Очевидно, что данная дробь не входит в рассматриваемую последовательность, поскольку от первого числа она отличается первой цифрой после запятой, от второго – второй цифрой и так далее. Следовательно, мы получили число из данного интервала, которое не пронумеровано и, таким образом, множество
и так далее. Очевидно, что данная дробь не входит в рассматриваемую последовательность, поскольку от первого числа она отличается первой цифрой после запятой, от второго – второй цифрой и так далее. Следовательно, мы получили число из данного интервала, которое не пронумеровано и, таким образом, множество 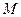 не является счётным. Его мощность называется континуум, а множества такой мощности называются континуальными. Приведённый метод доказательства называется диагональным методом Кантора.
не является счётным. Его мощность называется континуум, а множества такой мощности называются континуальными. Приведённый метод доказательства называется диагональным методом Кантора.
Следствие 1. Множество действительных чисел  континуально.
континуально.
Следствие 2. Множество всех подмножеств счётного множества континуально.
Как показывается в теории множеств (с помощью метода, аналогичного приведённому выше), для множества любой мощности множество всех его подмножеств (булеан) имеет более высокую мощность. Поэтому не существует множества максимальной мощности. Например, множество-универсум 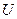 , описанное Кантором должно содержать все мыслимые множества, однако оно само содержится в множестве своих подмножеств в качестве элемента (парадокс Кантора). Получается, что множество
, описанное Кантором должно содержать все мыслимые множества, однако оно само содержится в множестве своих подмножеств в качестве элемента (парадокс Кантора). Получается, что множество 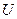 не является множеством максимальной мощности.
не является множеством максимальной мощности.
3. Отображения и функции.
Функцией называется любое функциональное соответствие между двумя множествами. Если функция 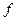 устанавливает соответствие между множествами А и В, то говорят, что функция
устанавливает соответствие между множествами А и В, то говорят, что функция 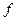 имеет вид
имеет вид 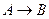 (обозначение
(обозначение 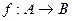 ). Каждому элементу
). Каждому элементу 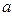 из своей области определения функция ставит в соответствие единственный элемент
из своей области определения функция ставит в соответствие единственный элемент 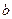 из области значений. Это записывается в традиционной форме
из области значений. Это записывается в традиционной форме 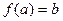 . Элемент
. Элемент 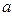 называется аргументом функции, элемент
называется аргументом функции, элемент 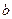 - её значением.
- её значением.
Полностью определённая функция 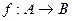 называется отображением А в В; образ множества А при отображении обозначается
называется отображением А в В; образ множества А при отображении обозначается 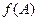 . Если при этом
. Если при этом 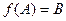 , то есть соответствие сюръективно, говорят, что имеет отображение А на В.
, то есть соответствие сюръективно, говорят, что имеет отображение А на В.
Если 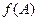 состоит из единственного элемента, то
состоит из единственного элемента, то 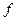 называется функцией-константой.
называется функцией-константой.
Отображение типа 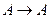 называется преобразованием множества А.
называется преобразованием множества А.
Пример 2.
а) Функция 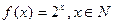 является отображением множества натуральных чисел в себя (инъективная функция). Эта же функция при всех
является отображением множества натуральных чисел в себя (инъективная функция). Эта же функция при всех 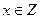 является отображением множества целых чисел в множество рациональных чисел.
является отображением множества целых чисел в множество рациональных чисел.
б) Функция 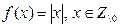 является отображением множества целых чисел (кроме числа 0) на множество натуральных чисел. Причём в данном случае соответствие не является взаимно однозначным.
является отображением множества целых чисел (кроме числа 0) на множество натуральных чисел. Причём в данном случае соответствие не является взаимно однозначным.
в) Функция 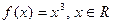 является взаимнооднозначным отображением множества действительных чисел на себя.
является взаимнооднозначным отображением множества действительных чисел на себя.
г) Функция 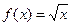 не полностью определена, если её тип
не полностью определена, если её тип 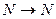 , но полностью определена, если её тип
, но полностью определена, если её тип 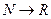 или
или 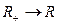 .
.
Определение. Функция типа  называется
называется 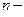 местной функцией. В этом случае принято считать, что функция имеет
местной функцией. В этом случае принято считать, что функция имеет 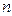 аргументов:
аргументов: 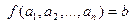 , где
, где 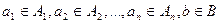 .
.
Например, сложение, умножение, вычитание и деление являются двухместными функциями на  , то есть функциями типа
, то есть функциями типа 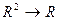 .
.
Определение. Пусть дано соответствие 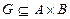 . Если соответствие
. Если соответствие  таково, что
таково, что 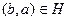 тогда и только тогда, когда
тогда и только тогда, когда 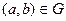 , то соответствие
, то соответствие 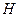 называют обратным к
называют обратным к 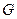 и обозначают
и обозначают 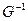 .
.
Определение. Если соответствие, обратное к функции 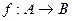 является функциональным, то оно называется функцией, обратной к
является функциональным, то оно называется функцией, обратной к 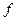 .
.
Очевидно, что в обратном соответствии образы и прообразы меняются местами, поэтому для существования обратной функции 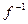 требуется, чтобы каждый элемент из области значения
требуется, чтобы каждый элемент из области значения 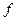 имел бы единственный прообраз. Это означает, что для функции
имел бы единственный прообраз. Это означает, что для функции 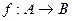 обратная функция
обратная функция 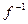 существует тогда и только тогда, когда
существует тогда и только тогда, когда 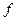 является биективным соответствием между своей областью определения и областью значений.
является биективным соответствием между своей областью определения и областью значений.
Пример 3. Функция 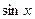 имеет тип
имеет тип 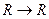 . Отрезок
. Отрезок 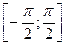 она взаимно однозначно отображает на отрезок
она взаимно однозначно отображает на отрезок 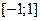 . Поэтому для неё на отрезке
. Поэтому для неё на отрезке 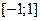 существует обратная функция. Как известно, это
существует обратная функция. Как известно, это 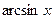 .
.
Определение. Пусть даны функции 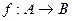 и
и 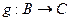 . Функция
. Функция 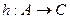 называется композицией функций
называется композицией функций 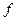 и
и 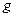 (обозначается
(обозначается 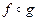 ), если имеет место равенство:
), если имеет место равенство: 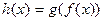 , где
, где 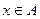 .
.
Композиция функций 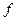 и
и 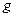 представляет собой последовательное применение этих функций;
представляет собой последовательное применение этих функций; 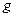 применяется к результату
применяется к результату 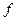 .Часто говорят, что функция
.Часто говорят, что функция 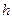 получена подстановкой
получена подстановкой 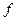 в
в 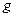 .
.
Для многоместных функций  возможны различные варианты подстановок
возможны различные варианты подстановок 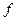 в
в 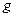 , дающие функции различных типов. Особый интерес представляет случай, когда задано множество функций типа:
, дающие функции различных типов. Особый интерес представляет случай, когда задано множество функций типа: 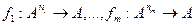 . В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов. Функция, полученная из данных функций
. В этом случае возможны, во-первых, любые подстановки функций друг в друга, а во-вторых, любые переименования аргументов. Функция, полученная из данных функций 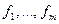 некоторой подстановкой их друг в друга и переименованием аргументов, называется их суперпозицией.
некоторой подстановкой их друг в друга и переименованием аргументов, называется их суперпозицией.
Например, в математическом анализе вводится понятие элементарной функции, являющейся суперпозицией фиксированного (не зависящего от значения аргумента) числа арифметических операций, а также элементарных функций ( 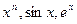 и т. п.).
и т. п.).
А.Н. Колмогоровым и В.И. Арнольдом доказано, что всякая непрерывная функция 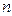 переменных представима в виде суперпозиции непрерывных функций двух переменных.
переменных представима в виде суперпозиции непрерывных функций двух переменных.
Замечание. Понятие функции широко используется в математическом анализе, более того, является в нём базовым понятием. В целом, подход к пониманию термина “функция” в матанализе несколько уже, чем в дискретной математике. Как правило, в нём рассматриваются так называемые вычислимые функции. Функция называется вычислимой, если задана процедура, позволяющая по любому заданному значению аргумента найти значение функции.
Лекция № 3. Отношения и их свойства.
1. Основные понятия и определения.
Определение. Подмножество 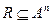 называется
называется  местным (
местным (  мерным) отношением на множестве А. Говорят, что элементы
мерным) отношением на множестве А. Говорят, что элементы 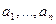 находятся в отношении
находятся в отношении  , если
, если 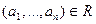 .
.
Одноместное (одномерное) отношение – это просто некоторое подмножество А. Такие отношения называют признаками. Говорят, что 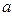 обладает признаком
обладает признаком  , если
, если 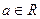 и
и 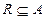 . Свойства одноместных отношений – это свойства подмножеств А, поэтому для случая
. Свойства одноместных отношений – это свойства подмножеств А, поэтому для случая 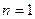 термин “отношения” употребляется редко.
термин “отношения” употребляется редко.
Наиболее часто встречающимися и хорошо изученными являются двухместные или бинарные отношения. Если 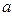 и
и 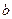 находятся в отношении
находятся в отношении  , это обычно записывается в виде
, это обычно записывается в виде 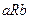 .
.
Пример 1. Бинарные отношения на множестве 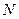 .
.
а) Отношение “ 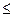 ” выполняется для пар
” выполняется для пар 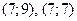 и не выполняется для пары
и не выполняется для пары 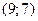 .
.
б) Отношение “иметь общий делитель, не равный единице” выполняется для пар 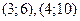 и не выполняется для пар
и не выполняется для пар 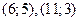 .
.
в) Отношение “быть делителем” выполняется для пар 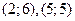 и не выполняется для пар
и не выполняется для пар 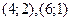 .
.
Пример 2. Бинарные отношения на множестве точек координатной плоскости.
а) Отношение “быть равноудалёнными от начала координат” выполнятся для пар точек 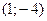 и
и 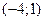 , но не выполнятся для пары точек
, но не выполнятся для пары точек 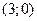 и
и 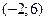 .
.
б) Отношение “принадлежать окружности, центр которой находится в начале координат”, выполняется для первой пары точек из предыдущего примера и не выполняется для второй пары.
в) Отношение “быть удалёнными на разное расстояние от начала координат” выполняется для всех точек, для которых не выполняется отношение, описанное в пункте “б”.
Пусть дано отношение  на множестве А. Для любого подмножества
на множестве А. Для любого подмножества 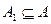 определяется отношение
определяется отношение 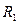 , называемое сужением
, называемое сужением  на
на 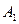 , которое получается из отношения
, которое получается из отношения  удалением всех пар, содержащих элементы, не принадлежащие
удалением всех пар, содержащих элементы, не принадлежащие 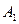 . Иначе говоря,
. Иначе говоря, 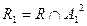 .
.
Строго говоря, само отношение  и его сужение
и его сужение 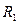 - это разные отношения, с разными областями определения. Однако, по умолчанию, если не возникает явных разночтений, эта разница не учитывается. Например, вполне можно говорить об отношении “быть делителем”, не уточняя, задано оно на множестве
- это разные отношения, с разными областями определения. Однако, по умолчанию, если не возникает явных разночтений, эта разница не учитывается. Например, вполне можно говорить об отношении “быть делителем”, не уточняя, задано оно на множестве 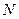 или на каком-нибудь его подмножестве.
или на каком-нибудь его подмножестве.
Для задания бинарных отношений можно использовать любые способы задания множеств (например, список пар, для которых данное отношение выполняется). Отношения на конечных множествах обычно задаются списком или матрицей. Матрица бинарного отношения на конечном множестве 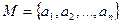 - это квадратная матрица
- это квадратная матрица 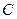 порядка
порядка 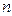 , в которой каждый элемент
, в которой каждый элемент 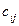 определяется следующим образом:
определяется следующим образом:
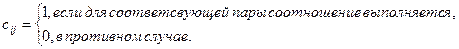
Пример 3. Для конечного множества 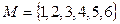 матрицы отношений из примера 1 (а – в) приведены в следующих таблицах.
матрицы отношений из примера 1 (а – в) приведены в следующих таблицах.
а)
б)
в)
Поскольку отношения на множестве А задаются подмножествами А2, для отношений можно определить те же операции, что и для множеств. Например, отношение “ 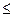 ” является объединением отношений “<” и “=”.
” является объединением отношений “<” и “=”.
Определение. Отношение 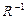 называется обратным к отношению
называется обратным к отношению  , если
, если 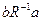 тогда и только тогда, когда
тогда и только тогда, когда 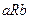 .
.
Непосредственно из определения следует, что 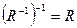 . Например, для отношения “
. Например, для отношения “ 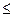 ” обратным является отношение “
” обратным является отношение “ 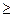 ”.
”.
2. Свойства отношений.
Определение. Отношение  называется рефлексивным, если для любого элемента
называется рефлексивным, если для любого элемента 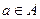 имеет место
имеет место 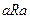 .
.
Главная диагональ матрицы рефлексивного отношения содержит только единицы.
Определение. Отношение  называется антирефлексивным, если ни для какого элемента
называется антирефлексивным, если ни для какого элемента 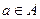 не выполняется
не выполняется 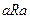 .
.
Главная диагональ матрицы рефлексивного отношения содержит только нули.
Например, отношения “ 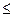 ” и “иметь общий делитель” являются рефлексивными. Отношения “
” и “иметь общий делитель” являются рефлексивными. Отношения “ 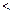 ” и “иметь сына” являются антирефлексивными. Отношение “быть симметричным относительно оси абсцисс” не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если лежит на этой оси, и не симметрична себе, если не лежит на ней.
” и “иметь сына” являются антирефлексивными. Отношение “быть симметричным относительно оси абсцисс” не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если лежит на этой оси, и не симметрична себе, если не лежит на ней.
Определение. Отношение  называется симметричным, если для любой пары
называется симметричным, если для любой пары 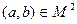 из отношения
из отношения 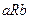 следует
следует 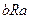 . Иными словами, отношение
. Иными словами, отношение  является симметричным тогда и только тогда, когда для любой пары
является симметричным тогда и только тогда, когда для любой пары 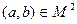 оно выполняется в обе стороны (или вовсе не выполняется).
оно выполняется в обе стороны (или вовсе не выполняется).
Матрица симметричного отношения симметрична относительно главной диагонали: 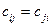 для любых
для любых 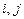 .
.
Определение. Отношение  называется антисимметричным, если из отношений
называется антисимметричным, если из отношений 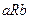 и
и 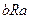 следует, что
следует, что 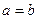 .
.
Отношение “быть симметричным относительно оси абсцисс” является симметричным: если первая точка симметрична второй относительно этой оси, то и вторая точка симметрична первой. Отношение “ 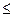 ” является антисимметричным. Действительно, если
” является антисимметричным. Действительно, если  и
и 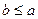 , это означает, что
, это означает, что 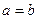 .
.
Нетрудно убедиться в том, что отношение  симметрично тогда и только тогда, когда
симметрично тогда и только тогда, когда 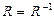 .
.
Определение. Отношение  называется транзитивным, если для любых
называется транзитивным, если для любых 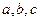 из отношений
из отношений 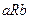 и
и 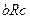 следует
следует 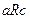 .
.
Отношения “быть равным”, “жить в одном городе”, “быть параллельным” являются транзитивными. Отношения “пересекаться”, “быть сыном” не являются транзитивными.
Замечание. В отличие от отношений рефлексивности и симметричности, для отношения транзитивности не формулируется противоположного понятия (антитранзитивности).
Определение. Транзитивным замыканием 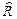 отношения
отношения  называется отношение, определяемое следующим образом: если в множестве
называется отношение, определяемое следующим образом: если в множестве 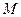 существует цепочка из
существует цепочка из 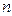 элементов
элементов 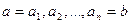 , в которой между каждыми двумя соседними элементами выполняется отношение
, в которой между каждыми двумя соседними элементами выполняется отношение  (
( 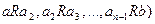 , то говорят, что существует транзитивное замыкание
, то говорят, что существует транзитивное замыкание 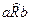 .
.
Замечание. Замыкание является весьма общим математическим понятием. Упрощённо говоря, замкнутость означает, что многократное повторение допустимых шагов не выводит за определённые границы. Например, множество натуральных чисел замкнуто относительно операции сложения, однако открыто (то есть незамкнуто) относительно операции деления.
Если отношение  транзитивно, то, очевидно,
транзитивно, то, очевидно, 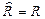 (и наоборот). Например, отношение “быть делителем” транзитивно для любой цепочки элементов и само является транзитивным замыканием этого отношения.
(и наоборот). Например, отношение “быть делителем” транзитивно для любой цепочки элементов и само является транзитивным замыканием этого отношения.
Если отношение  не транзитивно, то
не транзитивно, то 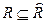 .
.
Например, транзитивным замыканием отношения “быть сыном” является отношение “быть прямым потомком”, включающее в себя понятия “быть сыном”, “быть внуком”, “быть правнуком” и так далее.
Лекция № 4. Основные виды отношений.
Из содержания предыдущей лекции и рассмотренных в ней примеров видно, что понятие “отношение” следует понимать весьма широко. В данной лекции мы попытаемся ввести определённую классификацию отношений и рассмотреть наиболее значительные с точки зрения математики виды отношений – а именно отношения эквивалентности и порядка.
- Отношения эквивалентности.
Определение. Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Пример 1.
а) Отношение равенства (часто обозначается  ) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы
) на любом множестве является отношением эквивалентности. Равенство – это минимальное отношение эквивалентности в том смысле, что при удалении любой пары из этого отношения (то есть любой единицы на главной диагонали матрицы  ) оно перестаёт быть рефлексивным и, следовательно, уже не является эквивалентностью.
) оно перестаёт быть рефлексивным и, следовательно, уже не является эквивалентностью.
б) Утверждения вида 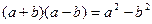 или
или 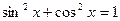 , состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “
, состоящие из формул, соединённых знаком равенства, задают бинарное отношение на множестве формул, описывающих суперпозиции элементарных функций. Это отношение обычно называется отношением равносильности и определяется следующим образом: две формулы равносильны, если они задают одну и ту же функцию. Равносильность в данном случае, хотя и обозначена знаком “=”, означает не то же самое, что отношение равенства, так как оно может выполняться для различных формул. Впрочем, можно считать, что знак равенства в таких отношениях относится не к самим формулам, а к функциям, которые ими описываются. Для формул же отношение равенства – это совпадение формул по написанию. Оно называется графическим равенством. Кстати, чтобы в подобных ситуациях избежать разночтений, часто для обозначения отношения равносильности используют знак “ 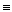 ”.
”.
в) Рассмотрим множество треугольников на координатной плоскости, считая, что треугольник задан, если даны координаты его вершин. Два треугольника будем считать равными (конгруэнтными), если при наложении они совпадают, то есть, переведены друг в друга с помощью некоторого перемещения. Равенство является отношением эквивалентности на множестве треугольников.
г) Отношение “иметь один и тот же остаток отделения на натуральное число 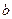 ” на множестве натуральных чисел является отношением эквивалентности.
” на множестве натуральных чисел является отношением эквивалентности.
е) Отношение “быть делителем” не является на множестве 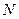 отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).
отношением эквивалентности. Оно обладает свойствами рефлексивности и транзитивности, но является антисимметричным (см. ниже).
Пусть на множестве 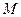 задано отношение эквивалентности
задано отношение эквивалентности  . Осуществим следующее построение. Выберем элемент
. Осуществим следующее построение. Выберем элемент 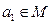 и образуем класс
и образуем класс 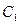 (подмножество
(подмножество 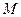 ), состоящий из элемента
), состоящий из элемента 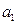 и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент
и всех элементов, эквивалентных ему в рамках данного отношения. Затем выберем элемент  и образуем класс
и образуем класс 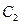 , состоящий из
, состоящий из 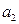 и эквивалентных ему элементов. Продолжая эти действия, получим систему классов
и эквивалентных ему элементов. Продолжая эти действия, получим систему классов 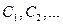 (возможно, бесконечную) такую, что любой элемент из множества
(возможно, бесконечную) такую, что любой элемент из множества 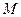 входит хотя бы в один класс, то есть
входит хотя бы в один класс, то есть 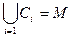 .
.
Эта система обладает следующими свойствами:
1) она образует разбиение множества 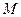 , то есть классы попарно не пересекаются;
, то есть классы попарно не пересекаются;
2) любые два элемента из одного класса эквивалентны;
3) любые два элемента из разных классов не эквивалентны.
Все эти свойства прямо следуют из определения отношения эквивалентности. Действительно, если бы, например, классы 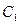 и
и 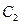 пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен
пресекались, то они имели бы хотя бы один общий элемент. Этот элемент был бы, очевидно, эквивалентен 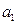 и
и 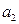 . Тогда, в силу транзитивности отношения
. Тогда, в силу транзитивности отношения  выполнялось бы
выполнялось бы 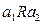 . Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.
. Однако, по способу построения классов, это не возможно. Аналогично можно доказать другие два свойства.
Построенное разбиение, то есть система классов – подмножеств множества 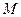 , называется системой классов эквивалентности по отношению
, называется системой классов эквивалентности по отношению  . Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение множества
. Мощность этой системы называется индексом разбиения. С другой стороны, любое разбиение множества 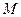 на классы само определяет некоторое отношение эквивалентности, а именно отношение “входить в один класс данного разбиения”.
на классы само определяет некоторое отношение эквивалентности, а именно отношение “входить в один класс данного разбиения”.
Пример 2.
а) Все классы эквивалентности по отношению равенства  состоят из одного элемента.
состоят из одного элемента.
б) Формулы, описывающие одну и ту же элементарную функцию, находятся в одном классе эквивалентности по отношению равносильности. В данном случае счётными являются само множество формул, множество классов эквивалентности (то есть индекс разбиения) и каждый класс эквивалентности.
в) Разбиение множества треугольников по отношению равенства имеет континуальный индекс, причём каждый класс имеет также мощность континуум.
г) Разбиение множества натуральных чисел по отношению “иметь общий остаток при делении на 7” имеет конечный индекс 7 и состоит из семи счётных классов.
- Отношения порядка.
Определение 1. Отношение  называется отношением нестрогого порядка, если оно является рефлексивным, антисимметричным и транзитивным.
называется отношением нестрогого порядка, если оно является рефлексивным, антисимметричным и транзитивным.
Определение 2. Отношение  называется отношением строгого порядка, если оно является антирефлексивным, антисимметричным и транзитивным.
называется отношением строгого порядка, если оно является антирефлексивным, антисимметричным и транзитивным.
Оба типа отношений вместе называются отношениями порядка. Элементы  сравнимы по отношению порядка
сравнимы по отношению порядка  , если выполняется одно из двух отношений
, если выполняется одно из двух отношений 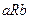 или
или 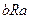 . Множество
. Множество 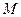 , на котором задано отношение порядка, называется полностью упорядоченным, если любые два его элемента сравнимы. В противном случае, множество называется частично упорядоченным.
, на котором задано отношение порядка, называется полностью упорядоченным, если любые два его элемента сравнимы. В противном случае, множество называется частично упорядоченным.
Пример 3.
а) Отношения “ 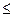 ” и “
” и “ 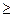 ” являются отношениями нестрогого порядка, отношения “<” и “>” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества
” являются отношениями нестрогого порядка, отношения “<” и “>” – отношениями строгого порядка (на всех основных числовых множествах). Оба отношения полностью упорядочивают множества 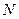 и
и  .
.
б) Определим отношения “ 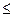 ” и “<” на множестве
” и “<” на множестве 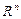 следующим образом:
следующим образом:
1) 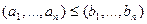 , если
, если 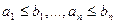 ;
;
2) 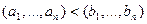 , если
, если 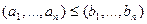 и при этом ходя бы для одной
и при этом ходя бы для одной 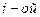 координаты выполняется
координаты выполняется 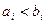 .
.
Тогда, например, 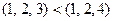 , но
, но 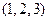 и
и 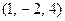 несравнимы. Таким образом, эти отношения частично упорядочивают
несравнимы. Таким образом, эти отношения частично упорядочивают 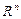 .,
.,
в) На системе подмножеств множества 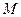 отношение включения “
отношение включения “ 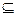 ” задаёт нестрогий частичный порядок, а отношение строгого включения “
” задаёт нестрогий частичный порядок, а отношение строгого включения “ 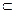 ” задаёт строгий частичный порядок. Например,
” задаёт строгий частичный порядок. Например, 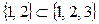 , а
, а 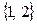 и
и 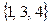 не сравнимы.
не сравнимы.
г) Отношение подчинённости в трудовом коллективе создаёт строгий частичный порядок. В нём, например, несравнимыми являются сотрудники различных структурных подразделений (отделов и т. п.).
д) В алфавите русского языка порядок букв зафиксирован, то есть всегда один и тот же. Тогда этот список определяет полное упорядочение букв, которое называется отношением предшествования. Обозначается 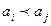 (
(  предшествует
предшествует 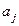 ). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.
). На основании отношения предшествования букв построено отношение предшествования слов, определяемое примерно, таким образом, как производится сравнение двух десятичных дробей. Это отношение задаёт полное упорядочение слов в русском алфавите, которое называется лексикографическим упорядочением.
Пример 4.
а) Наиболее известным примером лексикографического упорядочения слов является упорядочение слов в словарях. Например, 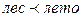 (так как
(так как 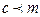 ), поэтому слово лес расположено в словаре раньше слова лето.
), поэтому слово лес расположено в словаре раньше слова лето.
б) Если рассматривать числа в позиционных системах счисления (например, в десятичной системе) как слова в алфавите цифр, то их лексикографическое упорядочение совпадает с обычным, если все сравниваемые числа имеют одинаковое количество разрядов. В общем же случае эти два вида могут не совпадать. Например, 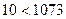 и
и 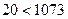 , но
, но 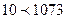 , а
, а 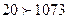 . Для того, чтобы они совпадали, нужно уравнять число разрядов у всех сравниваемых чисел, приписывая слева нули. В данном примере при этом получим
. Для того, чтобы они совпадали, нужно уравнять число разрядов у всех сравниваемых чисел, приписывая слева нули. В данном примере при этом получим 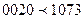 . Такое выравнивание происходит автоматически при записи целых чисел в ЭВМ.
. Такое выравнивание происходит автоматически при записи целых чисел в ЭВМ.
в) Лексикографическое упорядочивание цифровых представлений дат вида 19.07.2004 (девятнадцатое июля две тысячи четвёртого года) не совпадает с естественным упорядочением дат от более ранних к более поздним. Например, дата 19.07.2004 “лексикографически” старше восемнадцатого числа любого года. Чтобы возрастание дат совпадало с лексикографическим упорядочением, обычное представление надо “перевернуть”, то есть записать в виде 2004.07.19. так обычно делают при представлении дат в памяти ЭВМ.
Дата добавления: 2015-08-11; просмотров: 1196;
