А Ì В. Определение. Если А Í В, то множество А называется подмножествоммножества В (также говорят, что В покрывает А)

Определение. Если А Í В, то множество А называется подмножествоммножества В (также говорят, что В покрывает А). Если при этом А ¹ В, то множество А называется собственным подмножеством множества В и обозначается А Ì В.

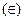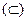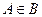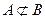Замечание. Не следует считать равносильными отношения принадлежности и вхождения одного множества в другое . Можно привести следующий пример. Пусть А – множество всех студентов данной группы, а В – множество всех учебных групп данного института. Здесь , но , поскольку элементы этих множеств разнородны. Этот пример показывает также, что элементами множеств могут являться другие множества.

Парадокс Рассела. Задание множеств характеристическим предикатом может привести к противоречиям. Рассмотрим множество всех множеств, не содержащих себя в качестве элемента: 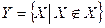. Если такое множество существует, то можно ответить на следующий вопрос: принадлежит ли оно само себе. С одной стороны, если 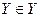, то 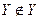. С другой стороны, если 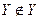, то 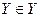! Это противоречие можно разрешить различными способами, в целом сводящимся к тому, что 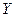не является множеством.

Для трех множеств А, В, С справедливы следующие соотношения:

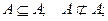
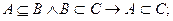
Связь между включением и равенством множеств устанавливается следующим соотношением:

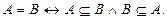
Здесь знак Ù обозначает конъюнкцию(логическое “и”).

В заключение добавим, что Г. Кантор предложил использовать понятие “универсального множества” (универсум), как бы противоположного понятию пустого множества 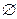. По мысли Кантора, универсальное множество 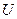содержит все мыслимые множества, и при этом оно само содержится во множестве своих подмножеств в качестве элемента. В дальнейшем смысл и содержание понятия универсального множества будут раскрыты более подробно.

2. Операции над множествами и их свойства.

Определение. Объединениеммножеств А и В называется множество С, элементы которого принадлежат хотя бы одному из множеств А и В.

Обозначается С = А È В.

А

В

Геометрическое изображение множеств в виде области на плоскости называется диаграммой Эйлера – Вэйна.

Определение. Пересечениеммножеств А и В называется множество С, элементы которого принадлежат каждому из множеств А и В.

Обозначение С = А Ç В.

А С В

Для множеств А, В и С справедливы следующие свойства:

А Ç А = А È А = А; A È B = B È A; A Ç B = B Ç A;

(A Ç B) Ç C = A Ç (B Ç C); (A È B) È C = A È (B È C);

A È (B Ç C) = (A È B) Ç (A È C); A Ç (B È C) = (A Ç B) È (A Ç C);

A È (A Ç B) = A; A Ç (A È B) = A;

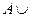Æ = А; A Ç Æ = Æ;

Определение. Разностьюмножеств А и В называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Обозначается: С = А \ В.

А В

Определение. Симметрической разностью множеств А и В называется множество С, элементы которого принадлежат в точности одному из множеств А или В.

Обозначается: А D В.

А D В = (A \ B) È (B \ A)

A B

Определение. С_Е называется дополнениеммножества А относительно множества Е, если А Í Е и C_Е = Е \ A.

A E

Для множеств А, В и С справедливы следующие соотношения:

A \ B Í A; A \ A = Æ; A \ (A \ B) = A Ç B;

A D B = B D A; A D B = (A È B) \ (A Ç B);

A \ (B È C) = (A \ B) Ç (A \ C); A \ (B Ç C) = (A \ B) È (A \ C);

(A È B) \ C = (A \ C) È (B \ C); (A Ç B) \ C = (A \ C) Ç (B \ C);

A \ (B \ C) = (A \ B) È (A Ç C); (A \ B) \ C = A \ (B È C);

(A D B) D C = A D (B D C); A Ç (B D C) = (A Ç B) D (A Ç C);

A È C_EA = E; A Ç C_EA = Æ; C_EE = Æ; C_EÆ = E; C_EC_EA = A;

C_E(A È B) = C_EA Ç C_EB; C_E(A Ç B) = C_EA È C_EB;

Пример 2. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера - Вэйна.

Из записанных выше соотношений видно, что

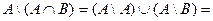Æ 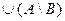= A \ В

Что и требовалось доказать.

Для иллюстрации полученного результата построим диаграммы Эйлера – Вэйна:

А В А В

AÇB

Пример 3. Исходя из определения равенства множеств и операций над множествами, доказать тождество.

A \ (B È C) = (A \ B) Ç (A \ C)

Если некоторый элемент х Î А \ (В È С), то это означает, что этот элемент принадлежит множеству А, но не принадлежит множествам В и С.

Множество А \ В представляет собой множество элементов множества А, не принадлежащих множеству В.

Множество А \ С представляет собой множество элементов множества А, не принадлежащих множеству С.

Множество (A \ B) Ç (A \ C) представляет собой множество элементов, которые принадлежат множеству А, но не принадлежат ни множеству В, ни множеству С.

Таким образом, тождество можно считать доказанным.

3. Векторы и прямые произведения.

Вектором (кортежем) в линейной алгебре и дискретной математике называют упорядоченный набор элементов. Это не есть определение вектора, поскольку целесообразнее это понятие считать основным.

Элементы, определяющие вектор, называются координатами или компонентами. Координаты нумеруются слева направо, а их число называется длиной или размерностью вектора. В отличие от элементов множества, координаты вектора могут совпадать. Координаты вектора заключаются в круглые скобки, например 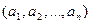. Иногда скобки или запятые опускаются. Часто векторы длины 2 называются упорядоченными парами, длины 3 – тройками и т. д.

Определение. Два вектора равны, если они имеют равную длину и их соответствующие координаты равны. Иначе говоря, векторы 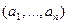и 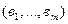равны, есл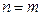и и .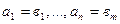

Определение. Прямым произведением множеств А и В (обозначение 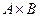) называется множество всех упорядоченных пар , таких, что 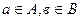. В частности, если А=В, то обе координаты принадлежат множеству А, такое произведение обозначается А². Аналогично, прямым произведением множеств 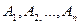называется множество всех векторов 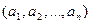длины п, таких, что .

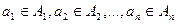Пример 4. Множество 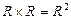- это множество всех упорядоченных пар действительных чисел, геометрической интерпретацией которого служит декартова координатная плоскость.

Координатное представление точек плоскости было впервые предложено Р. Декартом и исторически является первым примером прямого произведения. Поэтому часто прямое произведение множеств называют декартовым произведением.

Пример 5. Даны множества 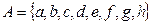и 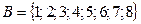. Тогда 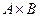есть множество обозначений клеток шахматной доски.

Вообще конечное множество, элементами которого являются какие-либо символы (буквы, цифры, знаки препинания, знаки операций и т. д.) называется алфавитом. Любые элементы множества 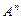в этом случае являются словами длины п в алфавите А. Например, десятичное целое число – это слово в алфавите цифр.

Определение. Проекцией вектора 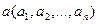на некоторую ось называется его компонента (координата) с соответствующим порядковым номером (обозначается пр_ia). Например, проекция точки плоскости на 1-ю ось есть её абсцисса (первая координата).

Теорема 1.1. Мощность произведения конечных множеств 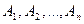равна произведению мощностей этих множеств: .

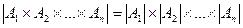Следствие. .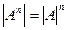

Эта простая теорема и её следствие впоследствии широко используются в комбинаторике.

Лекция № 2. Соответствия и функции.

1. Соответствия.

Определение. Соответствием между множествами А и В называется некоторое подмножество G их декартова произведения: .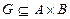

Если 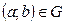, то говорят, что 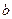соответствует 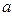при соответствии 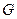. При этом множество всех таких 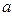называют областью определения соответствия 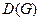, а множество соответствующих значений 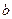называются областью значений соответствия .

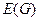В принятых обозначениях, каждый элемент 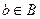, соответствующий данному элементу 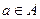называется образом 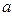при соответствии 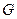, наоборот, элемент 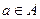называется прообразом элемента 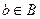при данном соответствии.

Соответствие называется полностью определённым, если 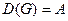, то есть каждый элемент множества 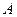имеет хотя бы один образ во множестве 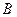; в противном случае соответствие называется частичным.

Соответствие 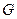называется сюръективным, если 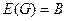, то есть если каждому элементу множества 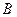соответствует хотя бы один прообраз во множестве .

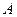Соответствие 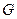называется функциональным (однозначным), если любому элементу множества 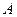соответствует единственный элемент множества .

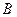Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества 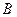имеет не более одного прообраза.

Соответствие 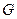называется взаимнооднозначным (биективным), если любому элементу множества 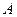соответствует единственный элемент множества 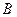, и наоборот. Можно сказать также, что соответствие является взаимнооднозначным, если оно является полностью определённым, сюръективным, функциональным, и при этом каждый элемент множества 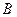имеет единственный прообраз.