Развертывающиеся линейчате поверхности

Линейчатыми называются поверхности, образованные движением прямой линии по определенному закону.

Развертывающимися (торсовыми) называются поверхности, которые можно развернуть на плоскости без складок и разрывов.

К развертывающимся линейчатым поверхностям относятся:

1. цилиндрическая;

2. призматическая;

3. коническая;

4. пирамидальная;

5. торсовая.

Данные линейчатые поверхности имеют одну направляющую.

Цилиндрическая поверхность Г(n, s) (Рис.21)

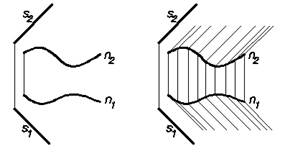
(n, s) –определитель поверхности.

Состав определителя:

n – направляющая (кривая линия);

s – направление образующей

(образующая – прямая линия).

Закон образования поверхности

(закон Каркаса):

li x n; li II s.

Рис.21

Призматическая поверхность L ( n, s) (Рис.22)

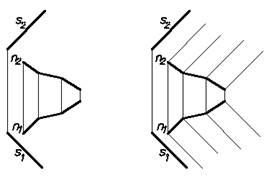(частный случай цилиндрической поверхности)

( n, s) –определитель поверхности.

Состав определителя:

n – направляющая (ломаная линия);

s – направление образующей

(образующая – прямая линия).

Закон образования поверхности

(закон Каркаса):

li x n; li II s.

Рис.22

Коническая поверхность D(n, S) (Рис.23)

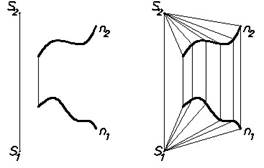
(n, S) –определитель поверхности.

Состав определите

n – направляющая (кривая линия);

S– вершина поверхности;

Закон образования поверхности:

li x n; li Ì s.

Рис.23

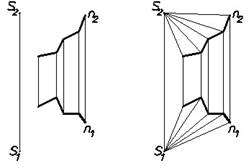Пирамидальная поверхность V(n,S) (Рис.24)

(частный случай конической поверхности, когдаобразующая – ломаная лини

( n, S) –определитель поверхности.

Состав определителя:

n – направляющая (ломаная линия);

S – вершина поверхности;

Закон образования поверхности:

Рис.24 li x n; li Ì S.

Лекция 4.

Поверхности с плоскостью параллелизма (поверхности Каталана ). Винтовые поверхности (Геликоиды ).