Задание плоскости на К.Ч.

Плоскость – простейший вид поверхности.

Плоскость – двумерный геометрический образ. Плоскости, как и все поверхности обозначаются прописными буквами греческого алфавита S,D,W,L,Y и т.д. Плоскость можно представить как совокупную последовательность положений прямой линии, перемещающейся в пространстве по двум параллельным прямым.

В отличие от точки или линии плоскость в общем случае не может быть задана своими проекциями на комплексном чертеже, т.к. горизонтальная, фронтальная и профильная проекции плоскости занимают все поле проекций П1, П2 и П3 комплексного чертежа. Поэтому для задания на К.Ч. плоскостей, а также других поверхностей введем понятие «определитель Г.О.»

Оопределитель Г.О.– сумма независимых геометрических условий, однозначно определяющих все множество точек данного Г.О. на К.Ч.

К примеру, для того, чтобы задать прямую линию на комплексном чертеже, достаточно задать на этом чертеже две точки этой линии. Таким образом, определителем прямой линии являются две точки, принадлежащие данной линии и заданные двумя своими проекциями на комплексном чертеже.

Плоскости на комплексном чертеже также могут быть заданы с помощью определителей.

Определители плоскостей общего положения (Рис.15).

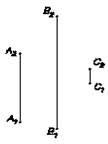1. Три точки, не лежащие на одной прямой L (А,В,С);

2. Прямая и точка, не лежащая на данной прямой S(а, C);

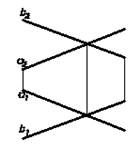3. Две пересекающиеся прямые D (ах b);

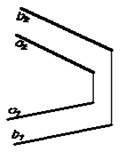4. Две параллельные прямые V ( aII b);

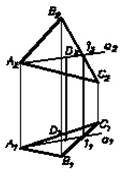5. Две проекции отсека плоской фигуры C(АВС).

Рис.15

Задание поверхностей с помощью определителей позволяет просто решать позиционные задачи на принадлежность одних геометрических образов другим.

На примере, приведенном на рис.15, решим задачу на принадлежность точки D плоскости C(АВС).

Дано:

C(АВС) –плоскость общего положения;

D(D2) - точка (DÌ C);D1 = ?