Плоскости частного положения.

Горизонтально проецирующая плоскость(Рис.16)

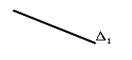Проекцией такой плоскости на П1 является прямая линия. Эта проекция называется главнойпроекцией плоскости D.

Проекцией плоскости D на П2 будут все точки фронтальной плоскости.

Рис.16

Фронтально- проецирующая плоскость (Рис.17)

Проекцией такой плоскости на П2 является прямая линия.

L2 - главная проекция плоскости L.

Рис.17

Главные проекции обладают собирательным свойством (проекции всех точек плоскости расположены на данной прямой).

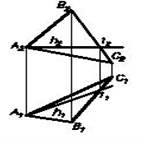Главные линии плоскости.

S(АВС) – плоскость общего

положения (Рис.18;

h – горизонталь плоскости S ;

h2^ А1А2 (А1А2 - линия связи);

все горизонтали плоскости S параллельны между собой.

Рис.18

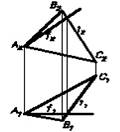
V(АВС) – плоскость общего положения (Рис.19);

f– фронталь плоскости V ;

f1^ А1А2(А1А2- линия связи);

все фронтали плоскости V параллельны между собой.

Рис.19

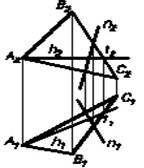C(АВС) – плоскость общего положения (Рис.20);

n (n1 ^ h1) - прямая наибольшего уклона плоскости C к горизонтальной плоскости проекций.

n (n2 ^ h2) прямая наибольшего уклона плоскости C к фронтальной плоскости проекций.

Рис.20

Прямые наибольшего уклона используются для измерения двугранного угла между плоскостью общего положения и плоскостью проекций. Задача сводится к измерению угла между соответствующей прямой наибольшего уклона и ее проекцией на заданную плоскость проекций.

Также необходимо заметить, что если на комплексном чертеже задана линия наибольшего наклона плоскости общего положения к плоскостям проекций, то можно утверждать, что на комплексном чертеже однозначно задана плоскость (определитель № 6). Доказательство этого вывода предлагается студентам выполнить самостоятельно.

Лекция 4. Развертывающиеся линейчатые поверхности (Р.Л.П. ). Задание Р.Л.П. на К.Ч.

Продолжение лекции 3.

Развертывающиеся линейчатые поверхности (Р.Л.П. ). Задание Р.Л.П. на К.Ч.