Плотность. Это одна из важнейших и широко употребляемых показателей качества нефтей и нефтепродуктов
Это одна из важнейших и широко употребляемых показателей качества нефтей и нефтепродуктов. На первых этапах развития нефтяной промышленности она была почти единственным показателем качества сырых нефтей, в частности, содержания керосина. Плотность определяется как масса единицы объема жидкости при определенной температуре (кг/м3, г/см3 или г/мл). На практике чаще используют относительную плотность - безразмерную величину, численно равную отношению истинных плотностей нефтепродукта и дистиллированной воды, взятых при определенных температурах. В качестве стандартных температур для воды и нефтепродукта приняты в США и Англии -15,6°С (60°F*), в других странах, в т.ч. у нас - 4°С и 20°С
*°F - градусы по шкале Фаренгейта, в которой температуры таяния льда и кипения воды приняты соответственно за 32 и 212 единиц; t °С = 5/9(t °F —32).
Определение плотности нефтяного сырья можно проводить при любой температуре (pt4), а затем вычислить значение р420 по формуле Д.И. Менделеева:
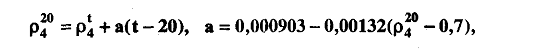
где а - средний температурный коэффициент расширения на один градус (его значения приводятся в справочной литературе, например: Расчеты основных процессов и аппаратов нефтепереработки: Справочник / Под ред. Е.Н. Судакова. М.: Химия, 1979.
Формула Д.И. Менделеева применима в сравнительно узком интервале температур от 0 до 50°С для нефтепродуктов, содержащих относительно небольшие количества твердых парафинов и ароматических углеводородов.
Плотность большинства нефтей в среднем колеблется от 0,81 до 0,90, хотя встречаются нефти легче или тяжелее указанных пределов. Плотности последовательных фракций нефти плавно увеличиваются. Плотность идентичных узких нефтяных фракций зависит от химического их состава и возрастает в зависимости от преобладания классов углеводородов в следующем порядке: алканы —>цикланы —> арены.
В некоторые формулы, применяемые в инженерных расчетах процессов нефтепереработки, входит значение плотности р420. Пересчитать ее можно по формуле
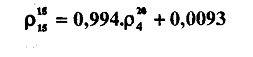
Дата добавления: 2015-08-11; просмотров: 1330;
