КИЭ кондиционера воздуха
= 40°C+273 = 313 
– температура наружного воздуха в жаркий день;
= 22°C+273 = 295 – температура в охлаждаемом кондиционером помещении.
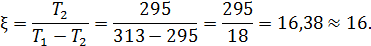
Значения КИЭ у реально существующих бытовых кондиционеров воздуха не превышают 3,5.
КИЭ теплового насоса
Поместив холодильник на улице, можно передавать количество теплоты от холодного воздуха за окном внутрь дома и обогревать его.
= 27°C+273 = 300 – температура в обогреваемом тепловым насосом помещении;
= -23°C+273 = 250 – температура наружного воздуха в зимнее время года.
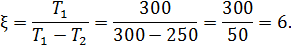
В действительности КИЭ бытовых тепловых насосов не превосходит 2,5.
Как видим эффективность теплового насоса, работающего с максимально допустимой эффективностью, составляет 600%. Это означает, что 1 Дж упорядоченной электрической энергии, подводимой к тепловому насосу позволяет передать от холодного воздуха за окном к теплому воздуху в доме 6 Дж энергии! Если же в качестве отопительного прибора использовать электрический тен, то КИЭ будет составлять 100%. Значит, использование теплового насоса оказывается в 6 раз эффективнее, чем использование традиционных электронагревательных приборов.
Тепловое загрязнение окружающей среды
В процессе работы любой тепловой машины часть получаемой от топлива энергии возвращается низкотемпературному резервуару (холодильнику). Эта энергия в конечном итоге полностью рассеивается и приводит к нагреву окружающей среды, т.е. атмосферы или прилегающих водоемов. Такой нагрев окружающей среды нежелательное явление с экологической точки зрения. Его называют тепловым загрязнением среды.
Контрольные вопросы
1. Что называется циклом Карно? Изобразите его график на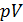 
диаграмме. Запишите формулу для КПД этого цикла.
2. Почему КПД машины Карно не может быть равным единице?
3. Почему в реальных машинах не используется цикл Карно?
4. Сформулируйте первую теорему Карно. Перечислите ее приложения.
5. Сформулируйте вторую теорему Карно. Перечислите ее приложения.
6. Сформулируйте принцип построения абсолютной термодинамической шкалы температур.
7. В чем заключается сущность метода циклов? Поясните на примере.
8. Получите неравенство Клаузиуса для цикла Карно. Запишите неравенство Клаузиуса в обобщенном виде. Для каких процессов неравенство переходит в равенство? Что из этого следует?
9. Сделайте оценку сверху КПД двигателя внутреннего сгорания, если температура воспламенения бензиново-воздушной смеси составляет 2000оС?
10. Сделайте оценку сверху КПД дизельного двигателя, если известно, что температура самовоспламенения дизельного топлива при сжатии равна 800оС.
11. Сделайте оценку сверху КИЭ бытового кондиционера, если температура наружного воздуха достигает 37оC, а в доме требуется поддерживать температуру 18оС.
12. Какое устройство называется тепловым насосом? Оцените его эффективность.
ЛЕКЦИЯ 11
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ.
Второе начало является решающей аксиомой термодинамики, поскольку именно оно определяет направление процессов, которые могут происходить в действительности. Кроме того, совместно с первым началом второе начало позволяет установить множество точных количественных соотношений между различными макроскопическими параметрами тел в состоянии термодинамического равновесия. Это оказывается возможным благодаря введению такого фундаментального понятия как энтропия. Энтропия (греч. – поворот, превращение) служит мерой преобразования или эволюции системы.
Исторически открытие второго начала связано с анализом работы тепловых машин, чем и определяются его исходные формулировки. Основоположником второго начала по праву считается Сади Карно. Подойдя вплотную ко второму началу, в своих знаменитых теоремах он не дал его чёткую формулировку. Это было сделано только в 1850-1851гг. независимо друг от друга Рудольфом Клаузиусом и Вильямом Томсоном (лордом Кельвином).
11.1. Формулировки второго начала термодинамики
К настоящему времени известно несколько десятков различных формулировок второго начала, большинство из которых носят запретительную форму, т.е. констатируют невозможность некоторых процессов и механизмов (машин). Таким образом, они отражают необратимость естественных процессов.
Ниже приведены три наиболее популярные формулировки постулата.
Формулировка Кельвина: невозможен циклический процесс, единственным результатом которого является производство работы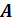 
за счет уменьшения внутренней энергии 
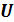только одного теплового резервуара (рис. 11.1).
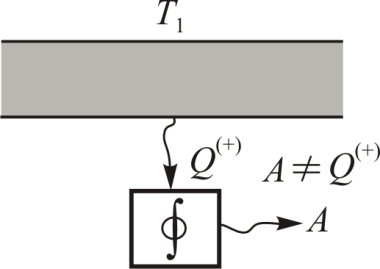Формулировка Оствальда: невозможен вечный двигатель второго рода. Вечный двигатель второго рода – это тепловая машина без низкотемпературного резервуара (рис 11.1).
| Рис. 11.1. |
Как видно, формулировки Кельвина и Оствальда по содержанию совпадают. И в той, и в другой предполагается, что для преобразования теплоты в работу необходима компенсация – отдача части количества теплоты, полученной рабочим телом, другим телам (холодильнику). Формулировка Клаузиуса вроде бы совсем про другое, в ней нет ни работы, ни двигателя. Несмотря на явные текстовые различия можно доказать эквивалентность формулировок Кельвина и Клаузиуса [12].
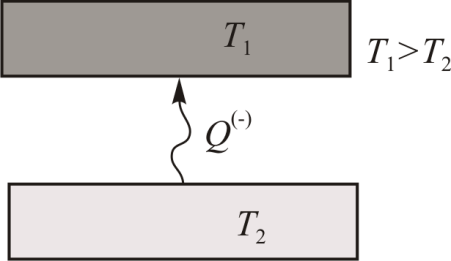Как уже отмечалось в 10.1 вечный двигатель первого рода запрещён первым началом
| Рис. 11.2. |
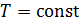, то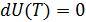 
, следовательно, уравнение первого начала примет вид
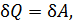
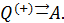
Совершать полное преобразование теплоты в работу циклически запрещает второе начало термодинамики, то есть оно запрещает существование вечного двигателя второго рода. Причём это утверждение не допускает обращения. Это означает, что, в то время как теплоту нельзя превратить в работу полностью (без компенсации), работу в теплоту можно превратить без всяких компенсаций. Существует фундаментальная асимметрия между теплотой и работой, хаосом и порядком. Эта универсальная концепция может быть выражена с помощью такого понятия как энтропия.
Современные формулировки второго начала термодинамики выражают закон существования энтропии у всякой равновесной системы и ее неубывания при любых процессах в изолированных системах. Первая часть формулировки - это определение энтропии по Клаузиусу (10.22), а вторая – закон возрастания энтропии. В некоторых учебниках [14,5] закон возрастания энтропии рассматривается как самодостаточная формулировка второго начала. Большую известность получила формулировка постулата в редакции А.Зоммерфельда. Она приведена ниже.
Энтропийная формулировка второго начала термодинамики
Часть первая
Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия данного состояния системы вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния (0) в соответствующее конечное состояние (1) через последовательность состояний равновесия. Вычисляются все подводимые при этом к системе порции теплоты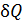 
, каждая из которых делится на соответствующую ей абсолютную температуру 
, и все полученные таким образом значения суммируются:
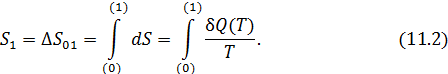
Часть вторая
При реальных (неравновесных) процессах энтропия замкнутой системы возрастает.
Информационное содержание постулата
• Энтропия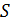 
есть функция состояния системы.
• Энтропия - величина аддитивная: энтропия макросистемы равна сумме энтропий её отдельных частей.
• Рост энтропии в изолированной системе означает нарастание хаоса и приближение системы к состоянию термодинамического равновесия. В этом состоянии S – максимальна, а dS=0. 
• В неизолированной системе энтропия может и возрастать, и убывать, и оставаться неизменной.
Заметим, что вторая часть приведенной выше формулировки постулата имеет строгое обоснование.
11.2. Закон возрастания энтропии в изолированных системах
Для того, чтобы получить заключение об изменении энтропии в процессах изолированной системы, необходимо провести определенную цепочку логических рассуждений.
Пусть замкнутая система, т.е. система теплоизолированная, переходит в некотором процессе из равновесного состояния 1 в равновесное состояние 2 (рис. 11.3). Возвратим систему с помощью обратимого процесса в состояние 1. При этом, конечно, необходимо ликвидировать изолированность системы.
В результате возвращения системы в состояние 1образовался цикл, к которому можно применить неравенство Клаузиуса
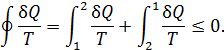
| Рис. 11.3. |
Учитывая особенности процессов, отметим, что первый интеграл обращается в нуль, поскольку система на этом участке цикла изолирована, значит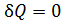 
. Второй интеграл можно в соответствии с определением энтропии для обратимых процессов записать в виде
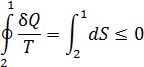
или
Следовательно
В контексте рассмотренной задачи неравенство (11.4) имеет единственный смысл: в процессах замкнутой системы энтропия не убывает. Полученный результат называют законом возрастания энтропии в изолированных системах. Знак равенства в (11.4) соответствует идеальным (равновесным) процессам, а знак неравенства – неравновесным процессам.
В качестве запоминающегося примера применения закона возрастания энтропии в процессах изолированной системы рассмотрим парадокс под названием «Демон Максвелла», сформулированный еще в 1879 году.
Демон Максвелла
Имеется изолированная система, представляющая собой некоторый сосуд, разделенный перегородкой на две половины, в одной из них находится газ, другая половина пустая.
«Демон» - живое разумное существо или техническое устройство, способное в изолированной системе пропускать через отверстие в перегородке «горячие» молекулы и не пропускать «холодные», т.е. открывать дверцу для одних и закрывать её для других (рис. 11.4).
Рис. 11.4.
Если кинетическая энергия молекулы, подлетающей к дверце, отвечает условию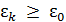 
, то ее будем считать горячей, если нет – то холодной. 
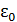– это наперед заданное значение энергии. В результате «работы» демона в одной половине сосуда ранее пустой соберутся горячие молекулы, а в другой – первоначально заполненной горячими и холодными молекулами, останутся только холодные молекулы.
Формулировка парадокса
Если существование демона возможно, то в изолированной системе возникает порядок, т. е. её энтропия уменьшается. Это противоречит второму началу термодинамики.
Разрешение парадокса
Существование демона невозможно по следующим причинам:
• Живое, а тем более разумное существо в изолированной системе погибнет. Даже если живой Демон что и успеет, то после его кончины хаос быстро восстановится. Если серьезно, то науке не известен биологический объект с требуемыми свойствами.
• Лёгкая дверца, которую может открыть только «энергичная» молекула, непременно будет броуновской частицей. Следовательно, она будет открываться и закрываться случайным образом и пропускать кого попало. Хаос сохранится, энтропия не уменьшится.
• Управление дверцей извне возможно, например, с помощью лазера, но тогда нарушается изолированность системы. В неизолированной системе энтропия может убывать, это не противоречит второму началу, но тогда условия «игры» не выполнены.
11.3. Область применимости второго начала термодинамики
Второе начало, как и термодинамика в целом, применимо к макросистемам при выполнении ряда исходных положений классической термодинамики [1]. Границы применимости постулата обозначены на схеме 11.3.1.
Схема 11.3.1.
| Границы применимости второго начала |
| Нижняя граница |
| Верхняя граница |
| • Законы термодинамики не применимы к микросистемам • Вечно движущаяся броуновская частица не есть вечный двигатель второго рода, поскольку макроскопическая работа не совершается • Для микросистем различие между теплотой и работой не существует, поэтому проблематика постулата теряет смысл. |
| • Существуют ограничения на применимость термодинамики к системам галактических размеров, вследствие определяющей роли в них дальнодействующих гравитационных сил • В соответствии с современными данными наблюдений Метагалактика представляет собой расширяющуюся систему и, следовательно, является нестационарной. Поэтому применимость второго начала на всю Вселенную неправомерна. |
Статистический характер второго начала
В статистической теории энтропия системы, находящейся в макроскопическом состоянии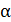 
, определяется формулой Больцмана
Рост энтропии в изолированной системе означает движение этой системы в направлении наиболее вероятного и стало быть равновесного состояния. В этом движении возможны флуктуации, в том смысле, что в какие-то короткие интервалы времени система может оказаться в менее вероятном макросостоянии, а, значит, ее энтропия ненадолго уменьшится.
Когда мы говорим о статистическом характере второго начала, то под этим понимаем, что не существует абсолютного запрета убывания энтропии в изолированной системе.
Чем больше число частиц в системе, тем меньше флуктуации и тем вероятнее выполняется закон возрастания энтропии. Термодинамика изучает макросистемы, содержащие огромное число частиц, в которых нарушение второго начала является практически невозможным событием.
11.4. Концепция тепловой смерти Вселенной
Заблуждения великих учёных не только занимательны, но и поучительны. Интересным образцом этого жанра является концепция «тепловой смерти». Вселенной, сформулированная почти полтора века назад на основе работ Клаузиуса. Являясь по своей идеологии ошибочной, она получила широкое распространение и долгие годы стимулировала более глубокое понимание научным сообществом второго начала термодинамики, а также общественный интерес к космологическим теориям, описывающим эволюцию Вселенной.
Концепция Клаузиуса
Клаузиус, рассматривая всю Вселенную как замкнутую систему, свел содержание второго закона термодинамики к утверждению: «Энтропия Вселенной стремится к максимуму». Когда этот максимум будет достигнут, во Вселенной прекратятся какие бы то ни было процессы. Таким образом, согласно Клаузиусу, во Вселенной в конце концов должно наступить абсолютно равновесное состояние, в котором никакие процессы уже невозможны. Такое состояние было названо тепловой смертью Вселенной.
Флуктуационная гипотеза Больцмана
Больцман рассматривал второе начало термодинамики как статистический закон. Отступления от равновесия – флуктуации, не только возможны, но и неизбежны. По Больцману неравновесное состояние Вселенной, в котором она находится сейчас, есть гигантская флуктуация. Эта флуктуация должна исчезнуть, тогда и наступит тепловая смерть Вселенной. Спустя некоторое время опять флуктуация – спонтанное рождение Вселенной. Затем опять смерть и так без конца. Времена между двумя последовательными флуктуациями невообразимо велики по сравнению со временем существования каждой из них. Поэтому Вселенная должна находиться в состоянии тепловой смерти почти всегда.
Несостоятельность концепции тепловой смерти Вселенной
Из-за тяготения однородное изотермическое распределение вещества во Вселенной не соответствует максимуму энтропии, поскольку такое состояние не является наиболее вероятным. Вселенная нестационарная. Первоначально однородное вещество распадается под действием сил тяготения, образуя звёзды, галактики, скопления галактик и т. д. Эти процессы происходят с ростом энтропии, никогда, однако, не приходя в состояние с максимумом энтропии, так как такого состояния вообще не существует.
11.5. Энтропия и её изменение в различных процессах
Расчет изменения энтропии в различных процессах макросистем зачастую является актуальной внутренней подзадачей разнообразных задач термодинамики, химии и биологии. В частности, изменение энтропии служит мерой изменения качества энергии. Важнейшим условием для тепловых машин, работающих по произвольному циклу, является условие их максимально допустимой эффективности. Это условие заключается в том, что процессы, лежащие в основе работы машин, являются равновесными (обратимыми) циклами, для которых выполняется равенство Клаузиуса
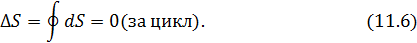
Если тепловая машина работает не по циклу Карно, но требуется достижение максимальной эффективности агрегата, надо выполнить это условие. Вы будете активно использовать это условие при решении учебных задач, а выдающийся советский физик лауреат нобелевской премии Петр Леонидович Капица добивался выполнения (11.6) при проектировании установок для сжижения гелия.
Вычислять изменение энтропии для обратимых процессов следует согласно (11.2). В подынтегральном выражении (11.2) 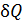можно представить двумя способами. Если известна теплоемкость 
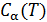в рассматриваемом процессе, то
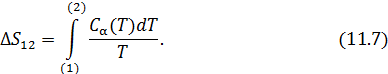
Если же о теплоемкости ничего не известно, то надо воспользоваться непосредственно первым началом термодинамики, тогда
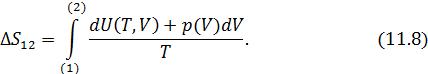
Применение (11.8) для идеального газа в количестве 1 моль приводит к формулам, имеющим широкое практическое использование
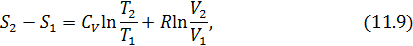
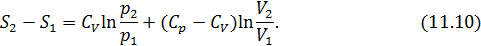
Большинство процессов, происходящих в природе, являются необратимыми. Для таких процессов вычисление энтропии основывается на том, что 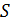– функция состояния. Если система перешла из одного состояния в другое необратимым образом, то можно мысленно заменить необратимый процесс обратимым, причем начальное и конечное состояния в этих процессах должны быть равновесными. Рассчитанное в этом случае изменение энтропии будет равно изменению энтропии при реальном необратимом процессе. Отметим, что воображаемый процесс не имеет ничего общего с реальным необратимым процессом, разумеется, кроме того, что у них совпадают начальные и конечные состояния. Обычно выбирают такой обратимый процесс, по которому расчёт проще.
Приведемпримеры необратимых процессов в теплоизолированных системах, которые часто встречаются в учебных задачах:
• Расширение идеального газа в вакуум (процесс Гей-Люссака).
• Диффузия (смешивание различных газов).
• Расширение газа через турбину с совершением работы.
• Процесс теплообмена двух и более тел.
Рассмотрим один из таких процессов подробнее.
Постановка задачи
Рассчитать изменение энтропии в процессе расширения идеального газа в вакуум в условиях адиабатической оболочки.
Описание системы
В сосуде объёмом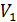 
при температуре находится идеальный газ в количестве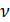 
молей (рис. 11.5). Если убрать перегородку, отделяющую объём 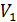от объёма 
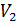, то начнется процесс расширения газа в вакуум.
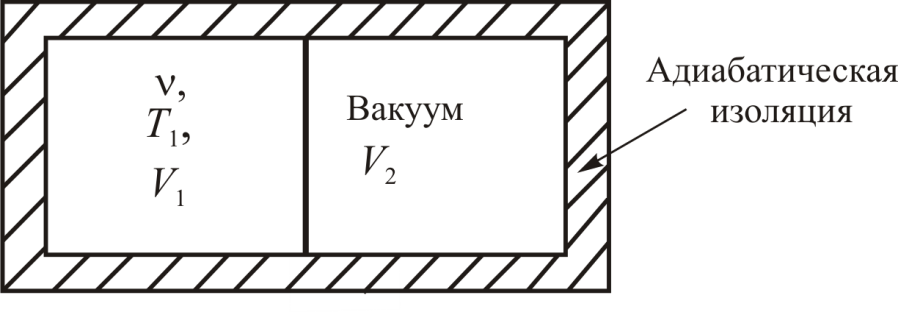
Рис. 11.5.
Актуальные свойства системы и процесса
• Процесс расширения газа в вакуум является необратимым. При быстром расширении давление газа зависит от координат и от времени.
• Газ расширяется в вакуум без совершения работы. Внешних сил нет, поэтому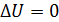 
и, следовательно, 
.
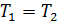• Для идеального газа справедливо уравнение Клапейрона-Менделеева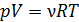 
.
Решение
Мысленно заменим неравновесный процесс на квазистатический изотермический процесс (рис. 11.6).
Рис. 11.6.
Обратите внимание на то, что в реальном процессе газ работу не совершает, а в фиктивном (воображаемом) процессе газ совершает изотермическую работу против внешних сил за счёт подводимого количества теплоты (изоляции нет!). Газ двигает поршень. Важно, что начальное и конечное состояния в том и другом процессе одинаковы и равновесны.
Для нахождения изменения энтропии воспользуемся формулой (11.8), тогда при условии, что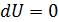 
, она примет вид
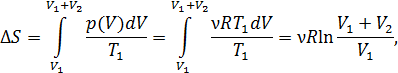
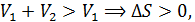
Ответ:
Как видно энтропия в процессе расширения идеального газа в вакуум в условиях тепловой изоляции возрастает. Полученная формула (11.11) может быть использована для вычисления изменения энтропии при диффузии идеальных газов и понимания замечательного факта, именуемого парадоксом Гиббса.
Парадокс Гиббса
Описание
Изолированная система представляет собой сосуд, разделенный перегородкой на две половины, в каждой из которых находится идеальный газ.
По разные стороны перегородки находятся различные газы.
Дата добавления: 2015-08-11; просмотров: 1288;