Приближенный расчет элементов дуги большого круга

Если при плавании по дуге большого круга менять курс судна нужно 1—2 раза в сутки (через 200—300 миль), то судно будет перемещаться не по дуге большого круга, а по близкой к ортодромии ломаной прямой. Точки С, D и т. д. (см. рис. 71), в которых происходит смена курсов, называют промежуточными точками. Курс судна, по которому оно следует от одной промежуточной точки до другой, называют промежуточным курсом.

Обозначим через D длину ортодромии между точками А и В.

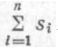
— длину ломаной прямой между точками А и В, где s1 = s2 = ... = sn — длина локсодромии между двумя промежуточными точками. Разность между

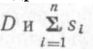
тем меньше, чем больше промежуточных точек выбрано на дуге большого круга. При расстоянии между промежуточными точками 200—300 миль эта разность прак- гически неощутима, т. е.

Si при s1 =s2 =..,=s n < 200/300 миль.

На практике поступают так. Вначале вычисляют значения начального и конечного курсов КН и КК по формулам сферической тригонометрии (сферический треугольник РпАВ):

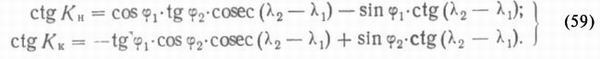
Если пункты отхода и прихода расположены в разных полушариях (северном и южном), то разность между начальным и конечным курсами (КН —КК) не представит величину полного изменения курса. В этом случае расчет производят дважды: первый — для плавания от пункта отхода до точки пересечения ортодромии с экватором; второй — для плавания от экватора до пункта прихода. Поэтому необходимо знать курс Ко, которым ортодромия пересекает экватор, и долготу точки пересечения λ0. Эти величины определяются по формулам сферической тригонометрии (прямоугольный сферический треугольник MBF):

tg (λ2 – λ0) = sin ϕ2 tg Kк sin K0 = cos ϕ2 sin Kк

Рассчитав КH и КK, далее вычисляют число п =

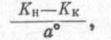
где а0 — целое число градусов (от 1 до 5°), а h — число равных отрезков дуги большого круга, каждый из которых можно пройти одним курсом при условии изменения этого курса на а° при переходе на следующий участок.

Затем вычисляют длину одного отрезка ломаной линии, т. е. длину плавания st между двумя промежуточными точками по локсодромии, считая

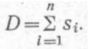
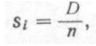
где Si — длина отрезка ломаной линии;

D — длина ортодромии.

Имея значения величин Si и п, плавание совершают следующим образом. В точке А судно ложится на ИК=КН. Пройдя этим курсом Si миль, судно меняет курс на а° и т. д. до прихода в точку В. Являясь самым коротким по расстоянию, плавание по ортодромии не всегда бывает самым выгодным. При выборе пути для большого океанского перехода решающее значение, кроме расстояния, имеют также гидрометеорологические условия. Так, может оказаться, что дуга большого круга ведет в такой район океана, где судно может встретиться с противным ветром, течением или со льдами. Поэтому кратчайший путь не всегда является наивыгоднейшим, особенно для судов со слабыми машинами (см. подробно в разделе «Лоция»),

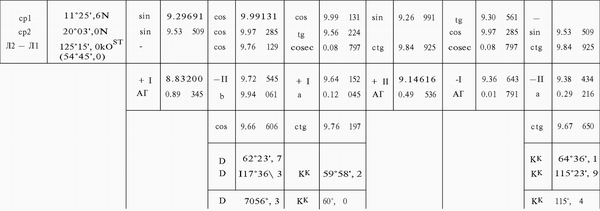
Пример 32. Для перехода из района Филиппинских островов φ=(1°2б', 6N и λ = 127°15',0 Ost) в район Калифорнийского залива (φ = 20°03', 0N и λ=107°30', 0W) рассчитать, через сколько миль плавания следует менять курс на величину а=2°,0.

Решение

1) Расчет величин D, Кп и Кк по формулам (58) и (59).

2) Расчет величин n и Si:

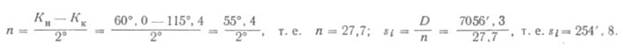
Ответ. Пройдя начальным курсом (Kн = 60°,0) расстояние 255 миль, судно должно менять курс на 2°,0 вправо и таким образом следовать до пункта назначения.