Плавание по дуге большого круга

Известно, что кратчайшим путем из одной точки на земной поверхности в другую является меньшая из дуг большого круга, проходящего через эти точки. Пусть судну надо перейти из точки А в точку В по дуге большого круга (рис. 71). Для этого нужно непрерывно менять курс судна от величины КН (курс начальный) до величины КК (курс конечный). Кроме того, дуга большого круга на меркаторской карте представлена кривой линией, обращенной своей выпуклостью к полюсу. Неудобство прокладки ортодромии на меркаторской карте, а также постоянная смена курса судна при следовании его по ортодромии осложняют плавание по дуге большого круга. Поэтому плавание по ортодромии совершается только при больших океанских переходах, когда расстояния между пунктами отхода и прихода по дуге большого круга и по локсодромии значительно (иногда на сотни миль) отличаются друг от друга.

Расчет длины ортодромии D (для сравнения ее с длиной локсодромии S) производят по формуле сферической тригонометрии (сферический треугольник РпАВ)

cos D = sin ϕ1 sin ϕ2 + cos ϕ1 cos ϕ2 cos (λ2 – λ1) (58)

где ϕ1 и λ1 —координаты точки А, а ϕ2 и λ2 — координаты точки В. Исследование формулы на знаки производят, считая положительными широту N и долготу Ost , а отрицательными широту S и долготу W.

Расчет длины локсодромии S производят по формулам письменного счисления.

Для того чтобы проложить дугу большого круга на морской карте, необходимо знать координаты нескольких промежуточных точек ортодромии, по которым можно было бы уверенно провести согласную кривую. Расчет координат промежуточных точек является трудоемким, требующим известного навыка и времени.

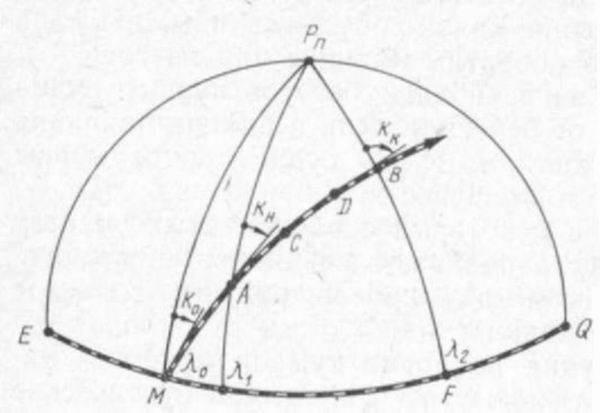
Рис. 71.

Вычерчивать точную проекцию дуги большого круга на карте нет смысла, так как судно во время плавания вследствие ряда причин (дрейф, течение и т. д.) будет лишь приближенно держаться намеченного пути. Поэтому при плавании по ортодромии чаще применяют приближенные приемы расчетов.