Расчет линейных цепей при несинусоидальных напряжениях и токах

Если напряжение, приложенное к цепи, имеет сложную форму:

,

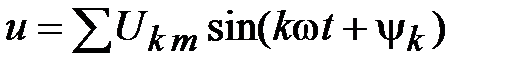то ток цепи с активным сопротивлением

,

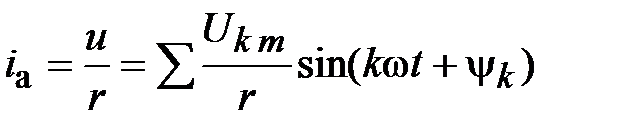ток в цепи с индуктивностью L

,

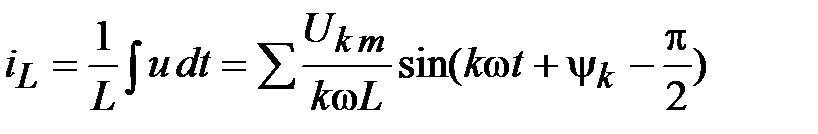ток цепи с емкостью С

.

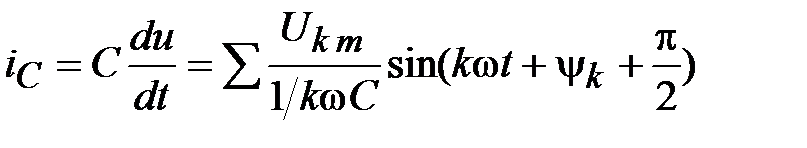Отсюда видно, что каждой гармонике напряжения соответствует своя гармоника тока, вычисляемая независимо от других гармоник.

При пренебрежении поверхностным эффектом активное сопротивление для всех гармоник одинаково. Индуктивное сопротивление 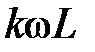растет, а емкостное - 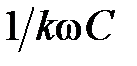убывает пропорционально порядку гармоники.

Таким образом, для расчета сложных линейных цепей может быть применен метод наложения: после разложения кривых заданных напряжений и токов в ряд Фурье задача решается для каждой гармоники в отдельности; при этом сопротивления ветвей для каждой гармоники в общем случае будут различными. Задачи для отдельных гармоник решаются однотипно и при их решении может быть использован весь аппарат теории синусоидальных токов – векторные диаграммы, символический метод и т. д. Затем можно произвести наложение решений для мгновенных значений отдельных гармоник – напряжений и токов каждой ветви и вычислить их действующие значения и мощность.