Напряжениях и токах
Действующее значение несинусоидального тока определяется, как и для синусоидального тока, по равенству средней мощности переменного тока и мощности постоянного тока в том же сопротивлении r.
 ,
,
т. е. действующее значение периодического переменного тока

является его среднеквадратичным значением за период. После подстановки в это выражение тока i в виде ряда Фурье:

Следовательно, 
т. е. действующее значение тока равно корню квадратному из суммы квадратов постоянной составляющей  и действующих значений токов всех гармоник, и не зависит от их начальных фаз
и действующих значений токов всех гармоник, и не зависит от их начальных фаз  .
.
По аналогии действующее значение напряжения  .
.
Важной характеристикой кривой является среднее значение ее абсолютной величины за период
 .
.
Например, для синусоиды
 .
.
Для характеристики кривых без постоянной составляющей пользуются несколькими коэффициентами.
Коэффициент искажения  равен отношению действующего значения первой гармоники к действующему значению всей кривой:
равен отношению действующего значения первой гармоники к действующему значению всей кривой:  ; в случае синусоиды
; в случае синусоиды 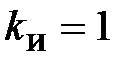 .
.
Коэффициент амплитуды 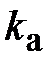 равен отношению максимального значения Um к действующему U:
равен отношению максимального значения Um к действующему U:  ; для синусоиды
; для синусоиды 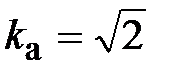 .
.
Коэффициент формы равен отношению действующего значения U ксреднему значению  кривой:
кривой:  ; для синусоиды
; для синусоиды  .
.
Мгновенная мощность р после разложения напряжения и тока в ряды Фурье получает вид:
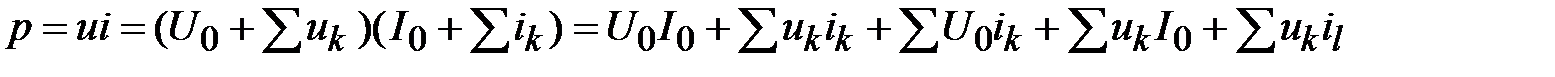 ,
,
т.е., кривая мгновенной мощности имеет весьма сложную форму, но средняя мощность равна сумме средних мощностей, создаваемых одноименными гармониками напряжения и тока:
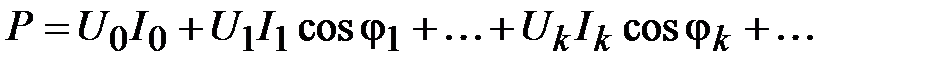 .
.
Дата добавления: 2015-08-11; просмотров: 634;
