Понятие о напряжениях
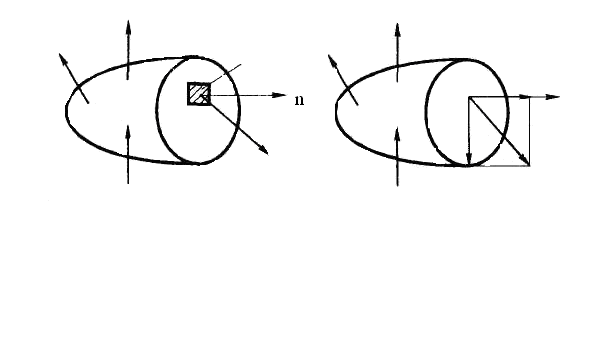
Внутренние силы, действующие в некотором сечении со стороны отброшенной части тела, можно привести к главному вектору и главному моменту. Выделим в рассматриваемом сечении с единичным вектором нормали и около точки М малую площадку DА (рис. 1.7 а).
| F1 |
| F3 |
| F1 |
| F3 |
| F2 |
| t |
| рn |
| s |
| F2 |
| М |
| DА |
| Dр |
а б
Рис. 1.7
Главный вектор внутренних сил, действующих на этой площадке, обозначим через Dр. Среднее напряжение на площадке DA будет
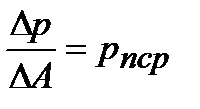 .
.
В пределе при DA® 0 получим напряжение в точке М
 .
.
Вектор полных напряжений рп зависит не только от действующих на тело внешних сил и координат рассматриваемой точки, но и от ориентации в пространстве площадки DA, характеризуемой вектором 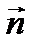 . Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора и определяет напряженное состояние в точке М.
. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора и определяет напряженное состояние в точке М.
В общем случае направление вектора полных напряжений рп не совпадает с направлением вектора нормали 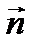 . Проекция вектора рп на направление нормали называется нормальным напряжением s, а на плоскость, проходящую через точку М и ортогональную вектору
. Проекция вектора рп на направление нормали называется нормальным напряжением s, а на плоскость, проходящую через точку М и ортогональную вектору 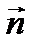 , – касательным напряжением t (рис 1.7 б).
, – касательным напряжением t (рис 1.7 б).
Нормальные напряжения возникают, когда частицы материала стремятся отдалиться друг от друга или, наоборот, сблизиться. Касательные напряжения связаны со сдвигом частиц по плоскости рассматриваемого сечения.
Очевидно, что
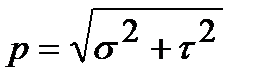 .
.
Касательное напряжение в свою очередь может быть разложено по направлениям осей ОУ и ОZ (txy, t.xz). Размерность напряжений – Н/м2.
Если вокруг точки А мысленно вырезать параллелепипед, то по его граням будет действовать совокупность напряжений, показанных на рис. 1.8. Нормальные и касательные напряжения в каждом поперечном сечении тела связаны определенным образом с внутренними усилиями, действующими в этом сечении. Если рассмотреть элементарную площадку dА поперечного сечения А бруса с действующими по этой площадке напряжениями s,tу, tz, получим, что на площадку dА действуют элементарные силы sdА, tуdА,tzdA. Тогда можно записать следующие интегральные зависимости:
N= 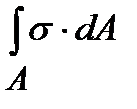 ;
; 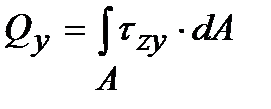 ;
; 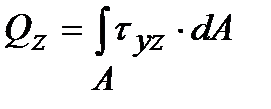
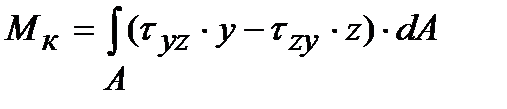 ;
;
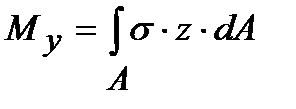 ;
; 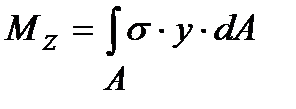 .
.
В сопротивлении материалов принято следующее правило знаков для напряжений. Нормальное напряжение s считается положительным, если совпадает по направлению с внешней нормалью п к площадке, и отрицательным, если его направление обратно.
Касательные напряжения t считаются положительными, если вектор касательных напряжении следует поворачивать против хода часовой стрелки до совпадения с внешней нормалью, и отрицательными – в противном случае (рис. 1.9).
Так как между напряжениями и внутренними усилиями существует интегральная связь, то правило знаков для внутренних силовых факторов обуслов лено принятым правилом знаков для нормальных sи касательных t напряжений. Моменты приняты положительными, как и ранее, если они действуют против хода часовой стрелки.
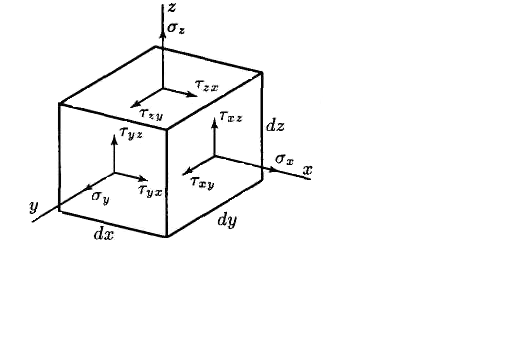
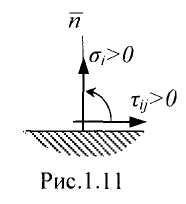
Рис. 1.8 Рис 1.9
Дата добавления: 2015-08-21; просмотров: 940;
