Внутренние силы
Между соседними частицами тела (кристаллами, молекулами, атомами) всегда действуют силы сцепления – внутренние силы. Эти силы стремятся сохранить тело как единое целое. Они препятствуют всякой попытке деформировать тело. Величина этих сил при нагружении тела и в ненагруженном его состоянии будет различной.
В сопротивлении материалов не рассматривают начальные внутренние силы в теле (в ненагруженном состоянии), а изучают дополнительные внутренние силы, которые появляются в результате нагружения тела. Внутренние силы часто называются усилиями.
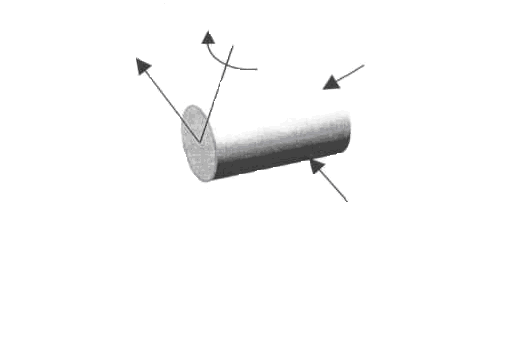
Для решения задачи о прочности надо уметь определять внутренние силы. Для этого в сопротивлении материалов широко применяют метод сечений. Сущность метода заключается в следующем. Пусть некоторое тело находится в равновесии под действием системы внешних сил (рис. 1.5 а).
Рассечем(мысленно) тело на две части плоскостью, перпендикулярной продольной оси тела (поперечным сечением).
Отбросимправую или левую часть тела. Чтобы оставшаяся часть находилась в равновесии, по плоскости сечения должны действовать внутренние силы.
Заменимдействие одной части на другую внутренними силами (рис. 1.5 б). Эти внутренние силы по характеру приложения – распределенные, в общем случае они не одинаковы по всему сечению. Внутренние силы могут быть приведены к их равнодействующим: главному вектору R и главному моменту М.
Введем ортогональную систему координат с началом в точке О,причем ось Х пусть совпадает с продольной осью тела, а оси Y и Z – с главными центральными осями инерции поперечного сечения (о них будет сказано ниже).
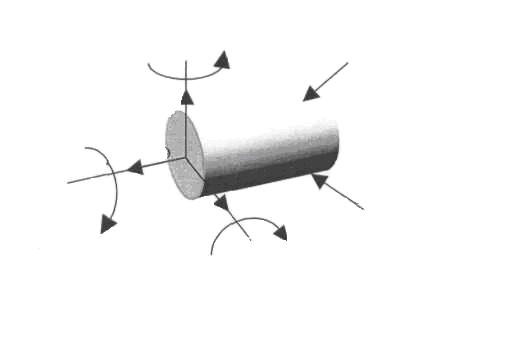
Разложим главный вектор R и момент М по осям (рис. 1.6). Получим шесть составляющих, которые называются внутренними силовыми факторами (ВСФ):
N –продольная (нормальная) сила, проекция вектора R на ось X;
Qz, Qy –поперечные силы, проекции вектора R на оси Z и Y соответственно;
Мх = Мк – крутящий момент, составляющая момента М вокруг оси X;
Mz, My – изгибающие моменты, составляющие момента М вокруг осей Z и Y соответственно.
| Fn |
| М |
| R |
| F3 |
| F3 |
| F1 |
| F2 |
| Fn |
| F3 |
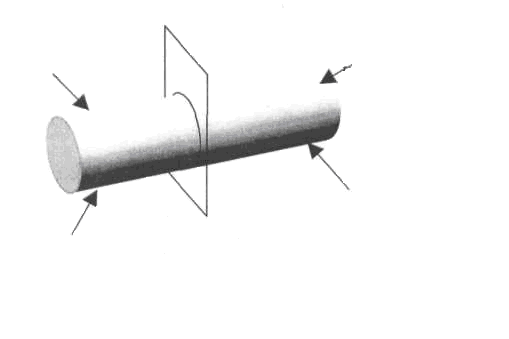
а б
Рис. 1.5
Рассмотрим правую часть.
|
| Мz |
| Fn |
| Z |
| X |
| My |
| F3 |
| Мх |
| y |
| F3 |
| О |
| N |
| Mк |
| Y |
Рис. 1.6
Уравновесим отсеченную часть. Так как отсеченная часть тела находится в равновесии, то для определения шести неизвестных ВСФ. составим шесть уравнений статического равновесия:
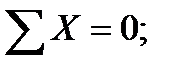
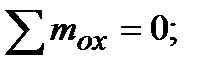
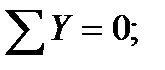

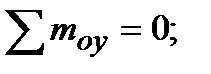
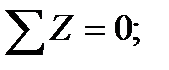
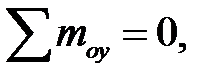
из которых поочередно определяются все ВСФ:
N = 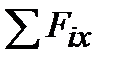 – нормальная сила равна сумме проекций всех внешних сил, дейст-
– нормальная сила равна сумме проекций всех внешних сил, дейст-
вующих на отсеченную часть, на продольную ось X;
Qy = 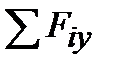 , Qz =
, Qz = 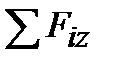 – поперечные силы равны по величине суммам проек-
– поперечные силы равны по величине суммам проек-
ций всех внешних сил, действующих на отсеченную часть, на
оси У и Z соответственно;
Mк =  – крутящий момент равен сумме внешних моментов, действующих
– крутящий момент равен сумме внешних моментов, действующих
на отсеченную часть, относительно оси Х;
Mу = 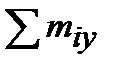 , Mz =
, Mz = 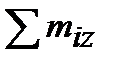 – изгибающие моменты равны суммам внешних момен-
– изгибающие моменты равны суммам внешних момен-
тов, действующих на отсеченную часть, относительно осей Y и Z
соответственно.
Для наглядного представления о характере работы конструкции строят графики изменения ВСФ по длине бруса (вдоль оси Х). Такой график принято называть эпюрой (от французского слова ерuге-чертеж).
Дата добавления: 2015-08-21; просмотров: 1333;
